Keyword: impurity, information gain, one-hot encoding for categorical features, sampling with replacement, random forest, XGboost, where to use decision trees
4.1 Decision trees
4.1.1 Decision tree model

- 입력 특징 X는 범주형 값(이산값)을 가지며, 목표 출력 Y는 고양이 여부(1 또는 0)입니다.
- 이는 이진 분류 작업으로, 이후에는 두 가지 이상의 값을 가지는 특징과 연속값 특징에 대해서도 다룰 것입니다.

- 결정 트리는 루트 노드에서 시작해 특징을 따라 좌우로 이동하며 최종 예측을 내린다.
- 각 노드는 특정 특징을 보고 분기하며, 최하단의 리프 노드는 최종 예측을 제공한다.
- 다양한 결정 트리 중에서 학습 알고리즘은 훈련 데이터와 교차 검증 데이터에서 잘 작동하는 트리를 선택한다.

3.1.2 Learning process


- 결정 트리를 학습할 때 중요한 첫 번째 결정은 각 노드에서 어떤 특징을 기준으로 분기할지 선택하는 것이다.
- 이를 위해 '순도'를 최대화하는 특징을 선택하는데, 이는 특정 특징을 기준으로 분기했을 때 결과 노드들이 가능한 한 모두 고양이 또는 모두 개가 되도록 하는 것을 의미한다.
- 다음 비디오에서는 불순도를 최소화하는 방법으로 엔트로피를 사용하는 방법을 다룰 것이다.

결정 트리를 구축할 때 두 번째 중요한 결정은 언제 분할을 멈출지 결정하는 것이다. 일반적으로 다음과 같은 기준을 사용한다:
- 모든 노드가 100% 고양이나 100% 개로 분류될 때.
- 트리가 최대 깊이에 도달할 때. 트리의 깊이는 루트 노드에서 해당 노드까지의 단계 수로 정의되며, 최대 깊이를 설정하여 트리가 너무 커지지 않도록 한다.
- 분할에 따른 순도 점수의 개선이 특정 임계값 이하일 때. 순도 개선이 너무 작으면 분할을 중단하여 트리가 과적합되지 않도록 한다.
- 노드의 예제 수가 특정 임계값 이하일 때. 예제 수가 적으면 분할을 중단하고 그 노드에서 예측을 만든다.
이러한 기준을 통해 트리가 너무 커지지 않고 과적합을 방지할 수 있다. 다음으로는 노드를 어떻게 분할할지에 대해 더 깊이 탐구할 것이다.
3.2 Decision tree learning
3.2.1 Measuring purity
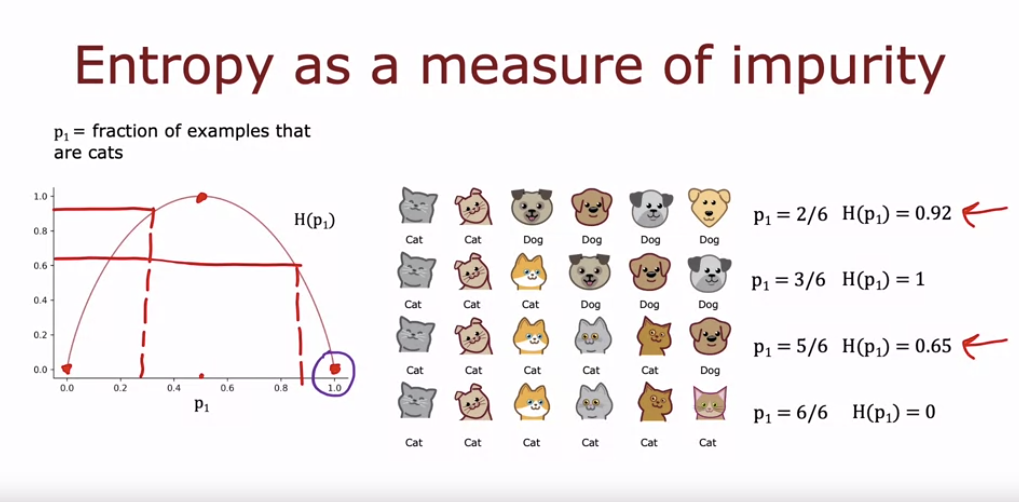
- 순도 측정을 위해 엔트로피를 사용한다. 엔트로피는 데이터 집합의 불순도를 나타내며, p_1은 양성 예제(고양이)의 비율을 나타낸다.
- 엔트로피는 p_1이 0.5일 때 가장 높아 1이 되고, 이는 불순도가 최대임을 의미한다. 반면, 예제가 모두 고양이이거나 모두 개일 때 엔트로피는 0이 되어 완전히 순수한 집합을 나타낸다.
- 예제 집합에서 p_1이 0.5에 가까울수록 불순도가 높고, p_1이 0이나 1에 가까울수록 불순도가 낮아진다.
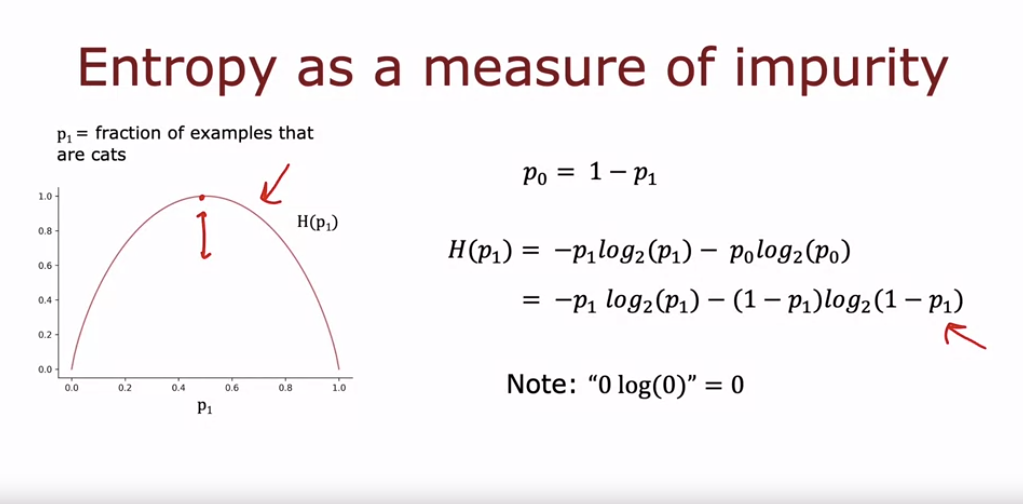
- 엔트로피 함수는 p_1이 0.5일 때 최대 1이 되고, p_1이 0 또는 1일 때 0이 된다. 이는 불순도가 가장 높은 경우와 가장 낮은 경우를 나타낸다.
- p_1 또는 p_0가 0인 경우, 0log(0)는 0으로 간주된다. 엔트로피 함수는 결정 트리의 노드에서 어떤 특징을 기준으로 분할할지 결정하는 데 사용된다.
- Gini 기준도 비슷한 목적으로 사용될 수 있지만, 이 강의에서는 엔트로피 기준에 중점을 둔다.
트로피 함수를 계산할 때 log의 base를 2로 사용하는 이유는 함수의 최고점을 1로 맞추기 위해서입니다. 이렇게 하면 함수가 더 해석하기 쉽고, 값이 이해하기 쉬운 범위 내에 있게 됩니다. 만약 base e(자연 로그)를 사용하면, 함수의 최고점이 1이 아닌 다른 값이 되어 숫자들이 직관적으로 이해하기 어려울 수 있습니다.
3.2.2 Choosing a split: information gain

- 의사 결정 나무를 구축할 때, 각 노드에서 어떤 특징으로 분할할지 결정하는 방법은 엔트로피를 가장 많이 줄이는 특징을 선택하는 것이다. 이는 **엔트로피 감소 또는 정보 이득(information gain)**으로 불린다.
- 각 분할의 엔트로피 값을 비교할 때, 단순히 엔트로피 값만 비교하는 대신 가중 평균 엔트로피를 계산하여 비교한다.
- 가중 평균 엔트로피는 각 가지의 엔트로피 값을 해당 가지로 분할된 예제 수의 비율로 가중하여 계산한다.
- 루트 노드에서의 엔트로피 값은 1이다. 정보 이득은 루트 노드의 엔트로피 값에서 가중 평균 엔트로피 값을 뺀 값으로 계산된다. 예를 들어, 귀 모양으로 분할했을 때 정보 이득은 0.28, 얼굴 모양으로 분할했을 때는 0.03, 수염 유무로 분할했을 때는 0.12가 된다. 가장 높은 정보 이득을 가지는 특징으로 분할하는 것이 좋다.
- 우리가 단순히 가중 평균 엔트로피를 계산하는 대신 엔트로피 감소량을 계산하는 이유는, 엔트로피 감소량이 너무 작으면 분할을 중단하는 기준으로 사용할 수 있기 때문이다.
- 엔트로피 감소량이 임계값보다 작으면 불필요하게 트리의 크기를 늘리고 과적합을 초래할 수 있으므로, 이러한 경우에는 분할을 중단하는 것이 바람직하다.
- 따라서, 이 예제에서는 귀 모양으로 분할하는 것이 가장 큰 엔트로피 감소를 가져오므로 루트 노드에서 귀 모양으로 분할하게 된다. 이와 같은 방법으로 각 노드에서 특징을 선택하여 나무를 구축한다.

- 정보 이득(information gain)의 공식 formula
3.2.3 Putting it all together

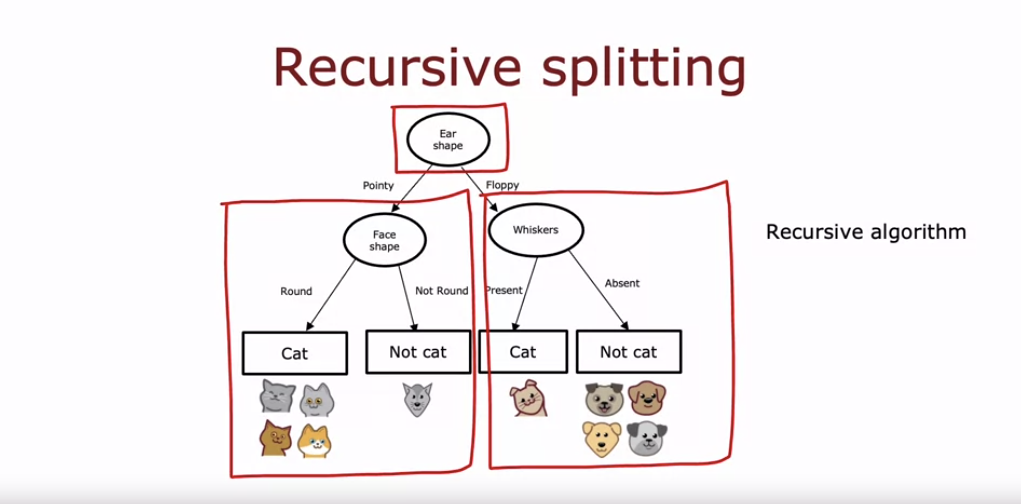
결정 트리를 구축하는 과정은 다음과 같다:
- 루트 노드에서 정보 이득을 계산하여 가장 높은 정보 이득을 가진 특성을 기준으로 분할한다. 예를 들어, 귀 모양이 가장 높은 정보 이득을 가지면 귀 모양을 기준으로 분할한다.
- 분할된 데이터에 대해 각 하위 트리에서 다시 정보 이득을 계산하여 최적의 특성으로 분할한다. 예를 들어, 왼쪽 하위 트리에서는 얼굴 모양이 최적의 특성이면 이를 기준으로 분할한다.
- 각 노드에서 모든 예시가 하나의 클래스에 속하거나 최대 깊이에 도달할 때까지 반복한다. 만약 특정 노드의 데이터가 모두 같은 클래스라면, 해당 노드는 예측을 위한 리프 노드가 된다.
- 오른쪽 하위 트리에서도 동일한 절차를 반복하여 트리를 완성한다.
- 이러한 절차는 재귀 알고리즘으로 구현되며, 각 하위 트리를 독립적으로 구축하여 전체 트리를 완성한다.
추가로, 최대 깊이 파라미터는 교차 검증을 통해 최적 값을 선택하거나(Although in practice, the open-source libraries have even somewhat better ways to choose this parameter for you), 정보 이득이 일정 임계값 이하일 때 분할을 중지하는 등의 방법으로 설정할 수 있다. 이를 통해 과적합을 방지하고 모델의 복잡성을 조절할 수 있다.
3.2.4 Using one-hot encoding of categorical features
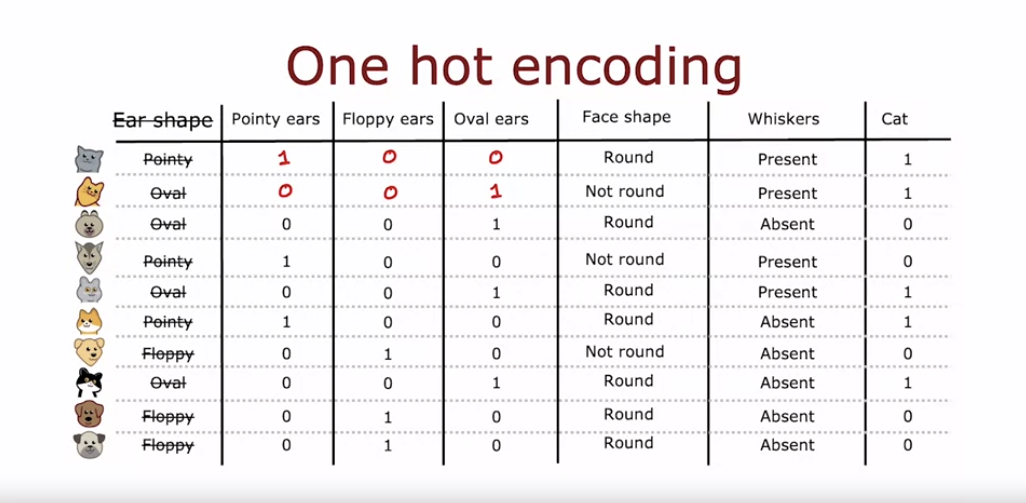

- 카테고리형 특성이 k개의 값을 가질 때, 이를 k개의 이진 특성으로 변환하여 각각 0 또는 1의 값을 가지도록 한다.
- 이 방법을 원-핫 인코딩이라 부르며, 각 행에서 정확히 하나의 값이 1이 된다. (그래서 one-hot encoding)
- 원-핫 인코딩은 결정 트리뿐 아니라 신경망, 로지스틱 회귀 등 다른 알고리즘에도 사용할 수 있다.
- 다음으로, 연속적인 값을 가지는 특성을 결정 트리에서 다루는 방법에 대해 알아보자.
3.2.5 Continuous valued features
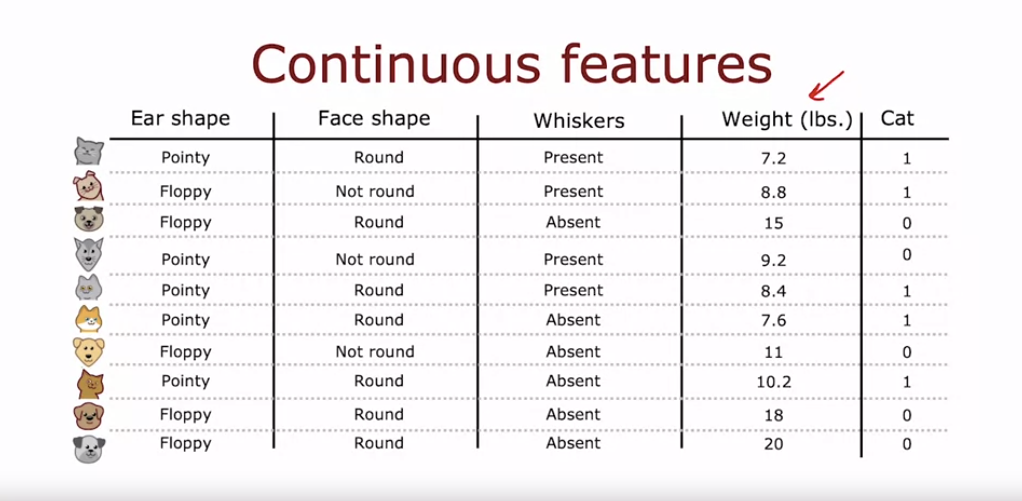

- 지금까지는 결정 트리를 사용하여 고양이인지 아닌지와 같은 분류 문제를 해결하는 방법에 대해 이야기했다.
- 하지만 숫자를 예측하는 회귀 문제를 다루고자 할 때, 다음 비디오에서는 이를 처리할 수 있는 결정 트리의 일반화 방법을 다룰 것이다.
3.2.6 Regression trees (optional)
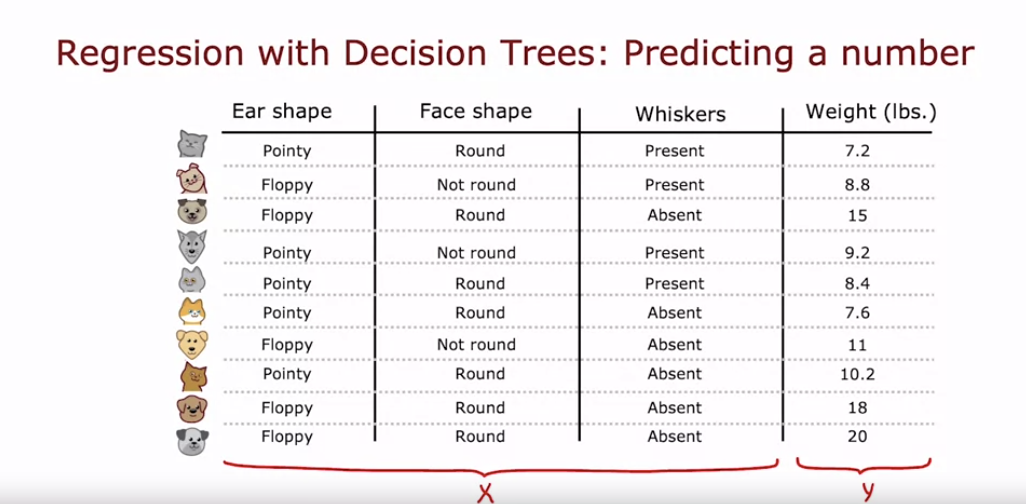
- 이번 영상에서는 이전에 사용한 세 개의 입력 특성을 이용해 동물의 무게를 예측하는 회귀 문제를 다룬다.
- 이 경우 무게는 입력 특성이 아닌, 예측하려는 목표 출력 Y이다
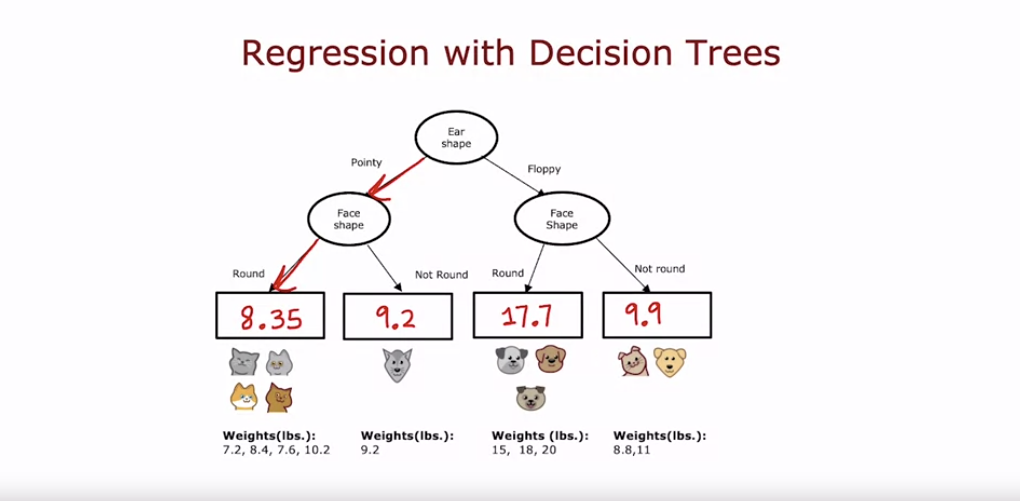
- 이를 위해 회귀 트리를 사용하며, 트리의 루트 노드는 귀 모양으로 분기하고, 이후 얼굴 모양으로 분기한다.
- 각 리프 노드는 해당 분기에 도달한 동물들의 무게 평균을 예측 값으로 사용한다.
- 예를 들어, 특정 분기에 7.2, 7.6, 10.2 무게의 동물이 도달하면, 해당 리프 노드는 무게의 평균인 8.35를 예측 값으로 출력한다.

- 회귀 문제를 다루는 의사결정 나무에서는 분류 문제와는 달리 분산을 감소시키는 것을 목표로 한다.
- 각 특징에 대해 분산을 계산하고 가중 평균 분산을 구한 후, 전체 데이터셋의 분산과의 차이를 계산하여 분산 감소량을 구한다.
- 예를 들어, 귀 모양을 기준으로 분할할 때 분산 감소량이 가장 컸다면, 귀 모양을 분할 기준으로 선택한다. 이후, 각 하위 집합에 대해 같은 방식으로 분할을 반복하여 최종 예측 모델을 완성한다.
- 다음 단계에서는 여러 개의 의사결정 나무를 결합한 앙상블 기법을 통해 더 나은 성능을 얻는 방법을 살펴볼 것이다.
3.3 Tree ensembles
3.3.1 Using multiple ensembles

- 단일 의사결정 나무는 데이터의 작은 변화에 매우 민감하다. 이를 해결하기 위해 여러 개의 의사결정 나무를 구축하는 방법인 앙상블 기법을 사용할 수 있다.
- 예를 들어, 예제가 [having pointy ears, round face, whiskers absent ⇒ floppy ears, round face, whiskers present] 이렇게 바뀐다면, 루트 노드에서 분할할 최고의 특징이 귀 모양에서 수염으로 바뀌고, 하위 트리도 완전히 달라진다.
- 이처럼 하나의 예제를 변경하면 전체 트리가 달라질 수 있어 단일 의사결정 나무는 안정성이 낮다.
- 따라서 더 정확한 예측을 위해 여러 개의 의사결정 나무를 사용하여 앙상블을 만드는 것이 좋다.
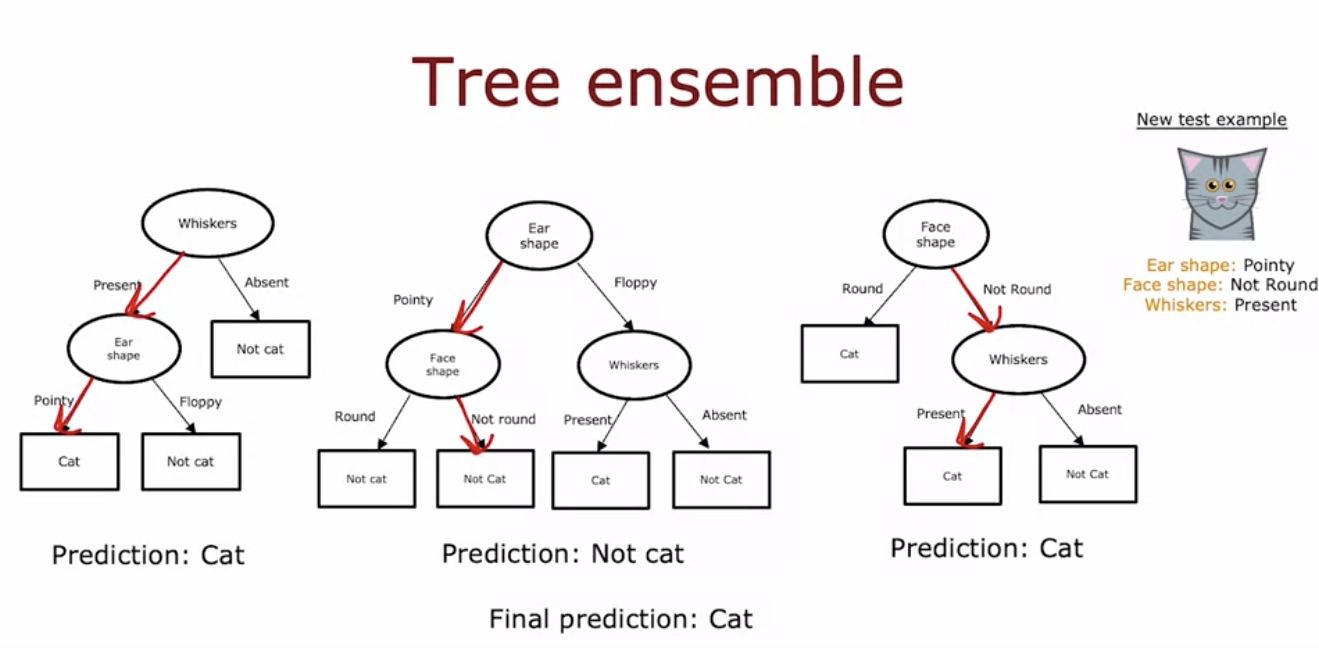
- 여러 개의 의사결정 나무를 모아 앙상블을 구성하면, 단일 나무의 예측에 대한 민감성을 줄이고 알고리즘의 안정성을 높일 수 있다.
- 새로운 예제가 주어졌을 때, 각 나무는 예측을 수행하고 다수결로 최종 예측을 결정한다.
- 예를 들어, 세 개의 나무 중 두 개가 '고양이'로 예측하면, 최종 예측은 '고양이'가 된다.
- 이러한 방법으로 앙상블을 구성하면, 개별 나무의 편향된 예측을 줄일 수 있다.
- 다음 비디오에서는 표본 복원 추출(Sampling with Replacement)이라는 통계 기법을 사용하여 여러 개의 다양한 의사결정 나무를 생성하는 방법을 설명할 것이다.
3.3.2 Sampling with replacement
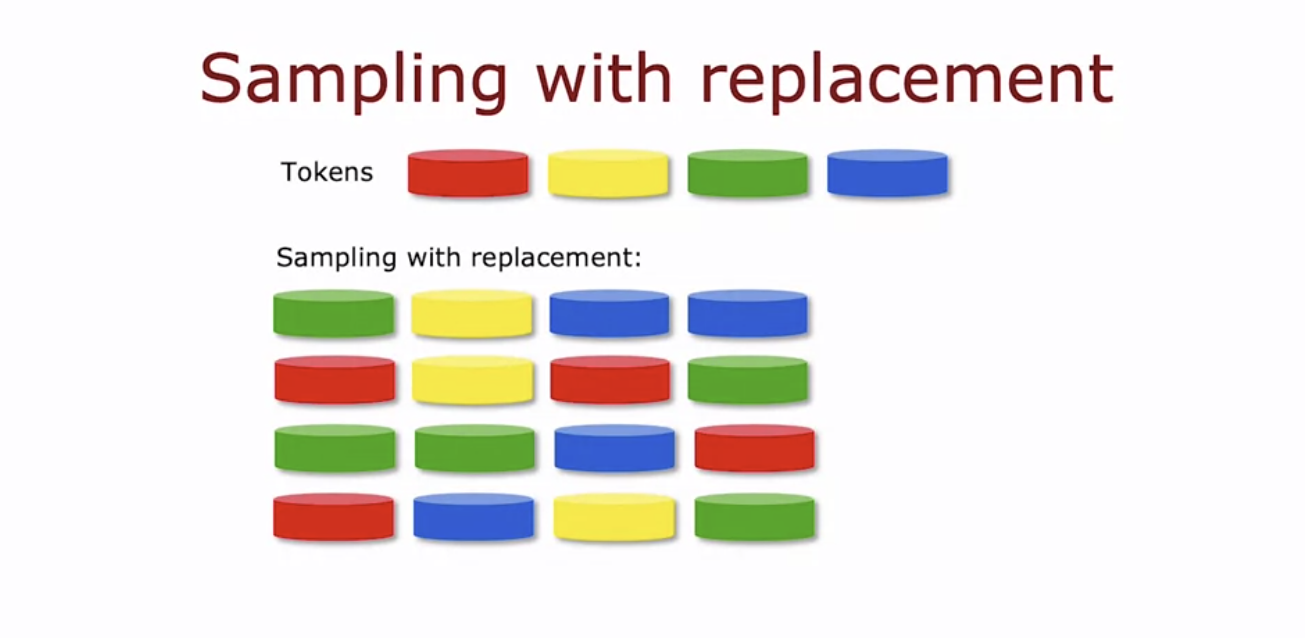
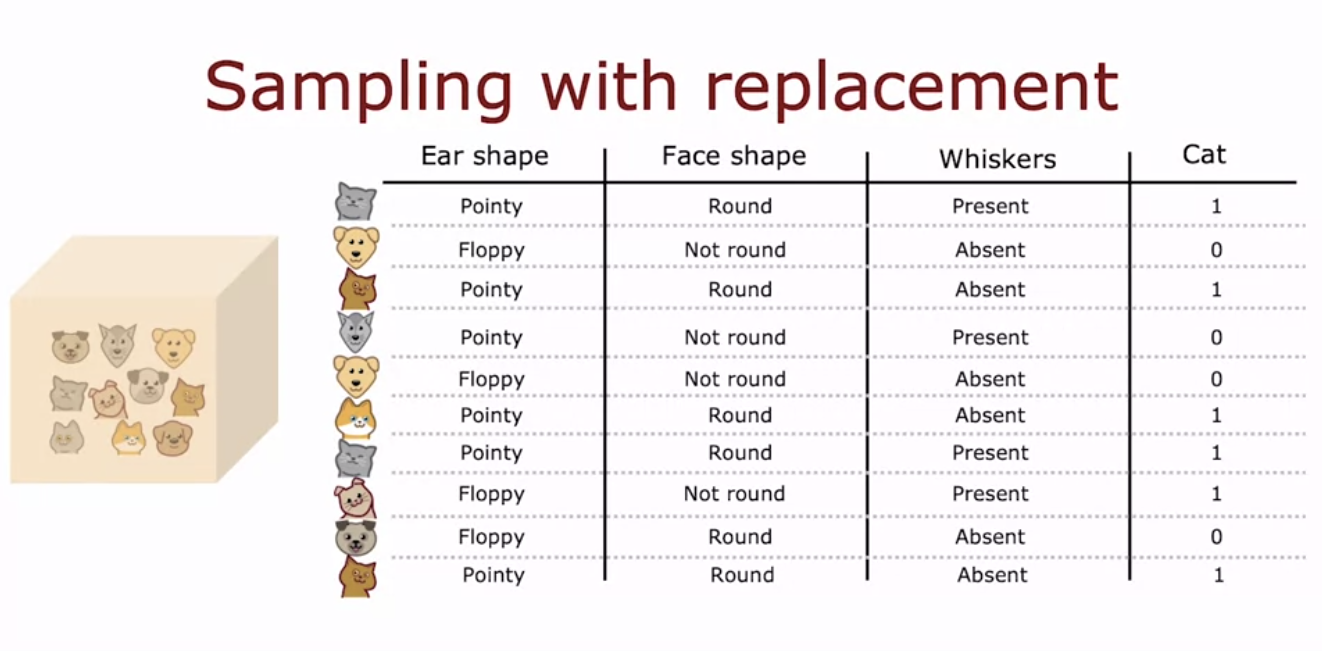
- 표본 복원 추출을 사용해 앙상블을 구성하는 방법은 다음과 같다.
- 먼저 원래 훈련 세트에서 여러 개의 무작위 훈련 세트를 생성한다.
- 원래 훈련 세트의 예제를 가방에 넣고, 무작위로 하나씩 뽑아 훈련 세트를 만든다.
- 뽑은 예제를 다시 가방에 넣고 반복하여 새로운 훈련 세트를 구성한다.
- 이렇게 하면 일부 예제는 반복될 수 있고, 원래 훈련 세트의 모든 예제를 포함하지 않을 수도 있다.
- 이러한 과정을 통해 원래 훈련 세트와 유사하지만 다른 무작위 훈련 세트를 여러 개 만들 수 있다.
- 이 방법은 여러 의사결정 나무를 생성하고 앙상블을 구성하는 데 중요한 역할을 한다.
3.3.3 Random forest algorithm

- 배경 결정 트리(Bagged Decision Tree) 알고리즘은 다음과 같다.
- 먼저, 표본 복원 추출을 통해 M개의 훈련 데이터를 가진 새로운 훈련 세트를 B번 생성한다.
- 각 훈련 세트마다 결정 트리를 훈련시켜 앙상블을 구성한다. 예측 시에는 모든 트리가 투표를 통해 최종 결과를 결정한다.
- 이 방식은 '배깅 결정 트리'로 불리며, 랜덤 포레스트는 트리의 초기 노드에서 다양한 특징을 선택해 더 나은 성능을 낸다.
- B값은 일반적으로 64~128 정도가 적당하다.
It turns out that setting capital B to be larger, never hurts performance, but beyond a certain point, you end up with diminishing returns and it doesn't actually get that much better when B is much larger than say 100 or so.

- 랜덤 포레스트 알고리즘은 배깅 결정 트리에 다음과 같은 수정사항을 추가하여 더욱 향상시킨다.
- 표본 복원 추출만으로는 루트 노드에서 항상 같은 분할을 선택할 수 있는데, 이를 방지하기 위해 각 노드에서 분할할 때 전체 N개의 특징 중 K개의 무작위 하위 집합에서만 선택하게 한다.
- 일반적으로 K는 N의 제곱근을 사용한다.
- 이 방법은 트리들이 서로 더 다르게 학습되도록 하여 앙상블의 정확도를 높인다.
- 이렇게 하면 작은 데이터 변경에 더 견고해지며, 결과적으로 랜덤 포레스트는 단일 결정 트리보다 훨씬 더 정확하고 안정적인 예측을 제공한다.
💡랜덤 포레스트가 배깅 결정 트리보다 더 안정적인 예측을 하는 이유: One way to think about why this is more robust to than a single decision tree is the sampling with replacement procedure causes the algorithm to explore a lot of small changes to the data already and it's training different decision trees and is averaging over all of those changes to the data that the sampling with replacement procedure causes. And so this means that any little change further to the training set makes it less likely to have a huge impact on the overall output of the overall random forest algorithm. Because it's already explored and it's averaging over a lot of small changes to the training set.
3.3.4 XGBoost

- XGBoost는 가장 널리 사용되는 결정 트리 앙상블 알고리즘으로, 빠르게 실행되며 많은 머신러닝 대회에서 성공적으로 사용되고 있다.
- 이 알고리즘은 배깅 결정 트리 알고리즘을 개선한 것으로, 매 반복마다 잘못 분류된 예제에 더 높은 확률을 부여하여 새로운 훈련 세트를 생성한다.
- 이를 통해 새로운 결정 트리가 이전 트리들이 잘못 분류한 예제들에 더 집중하게 한다.
- 이 방법은 피아노 연습에서 잘못 연주한 부분을 집중적으로 연습하는 '의도적 연습'과 유사하다.
- 이렇게 하면 학습 알고리즘이 더 빠르게 성능을 향상시킬 수 있다.
- Boosting 절차는 이 과정을 B번 반복하여 전체 모델의 성능을 향상시킨다.
- XGBoost는 이러한 boosting 기법을 구현한 가장 널리 사용되는 오픈 소스 라이브러리이다.

- XGBoost는 가장 널리 사용되는 부스팅 알고리즘 중 하나로, 매우 빠르고 효율적이며 오버피팅을 방지하기 위한 정규화 기능을 내장하고 있다.
- 머신러닝 대회에서 자주 사용되며 Kaggle과 같은 플랫폼에서 많은 대회를 우승하는 알고리즘이다.
- XGBoost는 기본 분할 기준과 분할 중지 기준이 잘 설정되어 있으며, 복원 추출 대신 각 훈련 예제에 다른 가중치를 부여하여 효율성을 높인다.

3.3.5 When to use decision trees (instead of neural networks)
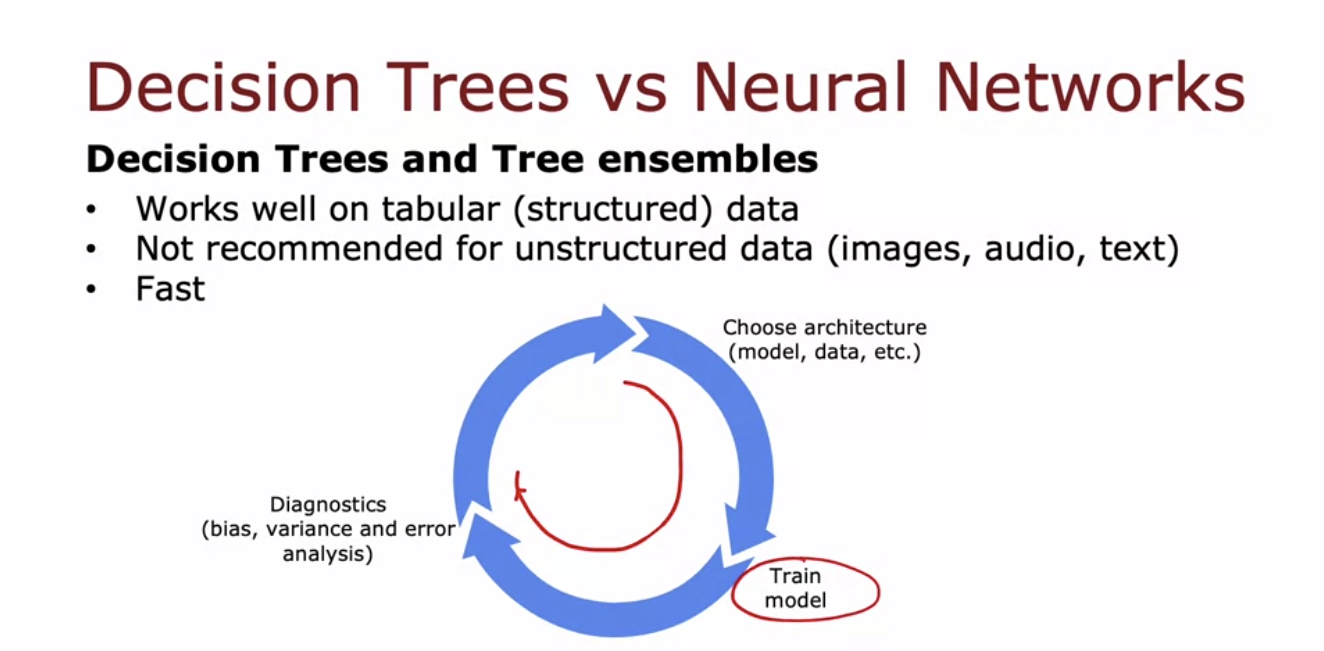
- 결정 트리와 트리 앙상블은 표 형식의 데이터(스프레드시트 형태의 데이터)에서 매우 효과적이다.
- 예를 들어, 주택 가격 예측에서는 집 크기, 침실 수, 층수, 집의 나이와 같은 특징이 포함된 데이터셋에서 잘 작동한다.
- 반면, 이미지, 비디오, 오디오, 텍스트와 같은 비정형 데이터에서는 신경망이 더 적합하다.
- 결정 트리의 큰 장점 중 하나는 훈련 속도가 빠르다는 점으로, 모델을 빠르게 훈련할 수 있어 반복적인 머신러닝 개발 과정을 더 효율적으로 진행할 수 있다.
- 마지막으로 작은 결정 트리의 경우 사람이 보고 직관적으로 이해할 수 있다는 장점이 있다. 그러나 트리 앙상블은 여러 트리와 많은 노드로 인해 해석이 어려울 수 있다. 트리 앙상블을 사용할 때는 주로 XGBoost를 추천하는데, 이는 성능이 뛰어나기 때문이다. 단일 결정 트리는 계산 비용이 적지만, 컴퓨팅 리소스가 제한되지 않는 한 XGBoost를 사용하는 것이 좋다.

- 신경망은 구조화된 데이터뿐만 아니라 이미지, 비디오, 오디오, 텍스트 같은 비구조화된 데이터에서도 잘 작동한다.
- 특히 신경망은 전이 학습이 가능해 작은 데이터셋에서도 큰 성능 향상을 기대할 수 있다.
- 단점으로는 큰 신경망은 훈련 시간이 오래 걸릴 수 있다는 점이다.
- 여러 신경망을 함께 사용하고 훈련시키는 것이 여러 결정 트리를 사용하는 것보다 쉽다.
- 이는 주로 신경망이 경사 하강법으로 함께 훈련될 수 있기 때문이다.
지도 학습 알고리즘은 레이블이 있는 데이터셋이 필요하지만, 레이블 없이도 유용한 패턴을 찾을 수 있는 강력한 비지도 학습 알고리즘도 있다. 이 과정의 다음 단계로 비지도 학습에 대해 배울 것이다.
impurity, information gain, one-hot encoding for categorical features, sampling with replacement, random forest, XGboost, where to use decision trees
'AI Study' 카테고리의 다른 글
| Advanced Learning Algorithms #3 (Advice for Applying Machine Learning) (0) | 2024.07.04 |
|---|---|
| Advanced Learning Algorithms #2 (Neural Network Training) (0) | 2024.07.02 |
| Advanced Learning Algorithms #1 (Neural Networks) (0) | 2024.07.01 |
| Supervised Machine Learning Regression and Classification #2 (0) | 2024.06.29 |
| Supervised Machine Learning Regression and Classification #1 (0) | 2024.06.26 |



