Keywords: Activation functions, Muliticlass classification, Softmax, Adam optimization, Numerical Roundoff Error, Back propagation(computation graph)
2.1 Neural Network Training
2.1.1 TensorFlow implementation
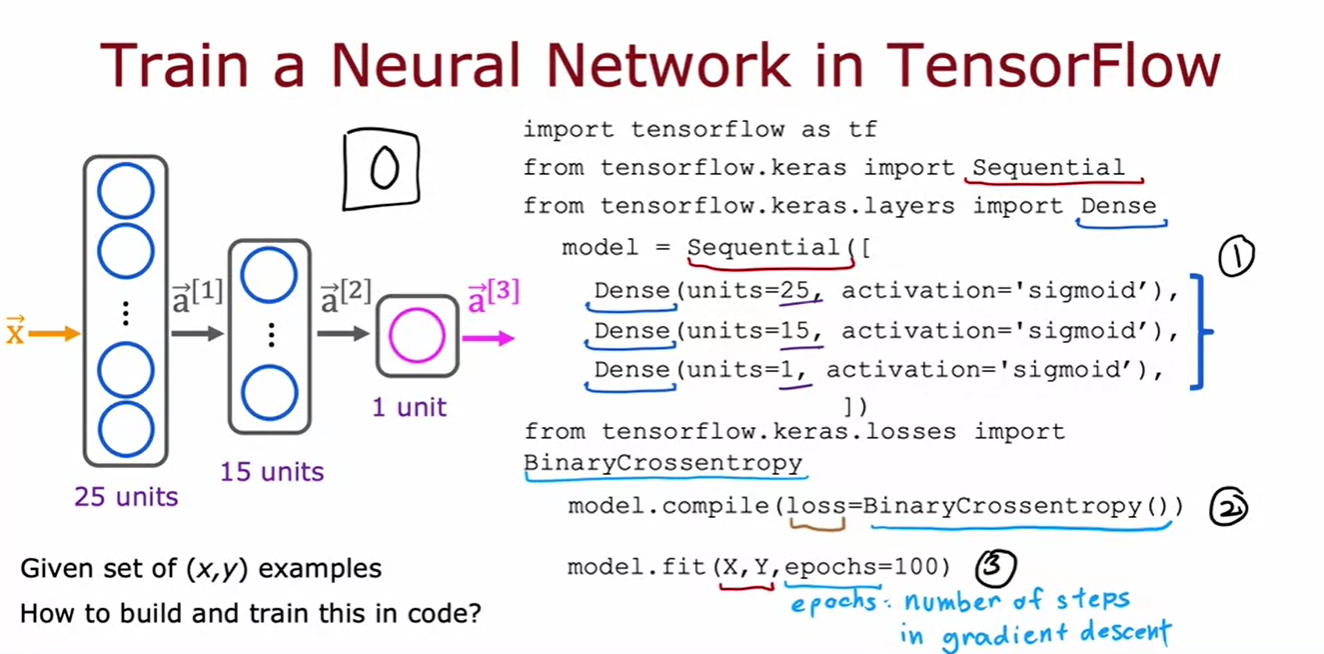
TensorFlow를 사용해 신경망을 훈련시키는 주요 단계는 다음과 같다:
- 모델 정의: Sequential 모델로 세 층(첫 번째 숨겨진 층 25개 유닛과 sigmoid 활성화 함수, 두 번째 숨겨진 층, 출력층) 구성.
- 모델 컴파일: 손실 함수로 binary crossentropy 지정.
- 모델 훈련: fit 함수를 사용해 데이터셋(X, Y)에 모델을 맞추고, 학습 반복 횟수(epochs)를 설정해 학습 실행.
이 단계를 이해하면 모델 훈련 중 문제가 발생할 때 디버깅에 도움이 된다.
2.1.2 Training details

[모델 학습 과정 개요]



- TensorFlow를 사용해 신경망을 훈련할 때, 모델 정의와 컴파일 후, model.fit을 호출하여 데이터를 학습시킨다.
- 이는 역전파(backpropagation) 알고리즘을 사용해 손실 함수의 파라미터를 최적화한다.
- TensorFlow는 이러한 과정을 자동으로 처리하며, 이는 과거에 직접 구현해야 했던 작업을 라이브러리로 간편하게 수행할 수 있게 해준다.
- 현대의 딥러닝 개발은 주로 TensorFlow나 PyTorch 같은 성숙한 라이브러리를 사용한다.
- forward propagation & backward propagation 정리 🔥🔥
- Forward Propagation: 입력 데이터를 신경망을 통해 전달하면서 각 층의 출력을 계산하고 최종 예측값을 얻는다. 이 예측값을 이용해 손실 함수를 계산한다.
- Backward Propagation: 손실 함수의 값을 기준으로 각 층의 파라미터(가중치와 편향)에 대한 기울기를 계산한다. 이는 체인 룰(chain rule)을 사용하여 네트워크의 마지막 층에서 처음 층까지 역방향으로 진행된다.
- 파라미터 업데이트: backward propagation을 통해 계산된 기울기를 사용하여 gradient descent 알고리즘에 따라 파라미터를 업데이트한다.
2.2 Activation Functions
2.2.1 Alternatives to the sigmoid function

- 신경망에서 awareness는 이진 값(0, 1)이나 0과 1 사이의 값이 아닌, 0부터 매우 큰 값까지의 비음수로 모델링하는 것이 더 적절할 수 있다. 이는 구매자가 약간, 어느 정도, 매우 인지하고 있거나 완전히 바이럴된 경우를 모두 표현할 수 있기 때문이다.
- 이러한 상황에서 활성화 함수로 ReLU 함수를 사용하면 더 강력한 모델을 만들 수 있다.
- 이는 ReLU 함수가 음수일 때 0, 양수일 때는 z 값을 그대로 반환하여, sigmoid 함수보다 비선형성을 잘 반영하고, gradient 소실 문제를 줄여 학습 속도와 성능을 향상시키기 때문이다.

- 위는 가장 많이 사용되는 활성화 함수이다.
- Linear activation function을 사용하는 경우, “우리는 활성화 함수를 사용하지 않는다”라고 표현하기도 한다.
2.2.2 Choosing Activation Functions

출력층의 활성화 함수를 선택할 때는 예측하려는 레이블 y에 따라 가장 적합한 함수가 있다.
- 이진 분류 문제: y가 0 또는 1인 경우, sigmoid 활성화 함수 사용.
- 회귀 문제: y가 양수 또는 음수가 될 수 있는 경우, 선형 활성화 함수(linear activation) 사용.
- 양수 값 예측 문제: y가 음수가 될 수 없는 경우(예: 집 값 예측), ReLU 활성화 함수 사용.
이 가이드는 출력층의 활성화 함수를 선택하는 데 있어 일반적으로 따르는 방법이다.

- 숨겨진 층의 활성화 함수로 ReLU 함수가 가장 일반적으로 사용된다.
- 이는 ReLU 함수가 sigmoid 함수보다 계산이 빠르고, gradient descent를 사용할 때 학습이 더 효율적이기 때문이다.
- ReLU는 그래프의 왼쪽만 평평한 반면, sigmoid는 양쪽이 평평하여 학습 속도가 느려질 수 있다.

2.2.3 Why do we need activation functions

- 하나의 숨겨진 유닛과 하나의 출력 유닛을 가진 신경망에서, 모든 활성화 함수로 선형 함수 g(z)=z를 사용하면, 출력 a2는 입력 x의 선형 함수가 된다.
- 이는 수학적으로 a2=w⋅x+b와 같아져, 결국 선형 회귀 모델과 동일한 결과를 낳는다.
- 따라서, 선형 활성화 함수를 사용하면 여러 층을 추가해도 복잡한 기능을 학습할 수 없다.

- hidden layers의 activation function을 linear activation function을 사용하고 output layer의 activation function을 sigmoid로 한다면 이건 logistics regression과 동일한 결과를 낳는다.
- So Don’t use linear activations in hidden layers!
2.3 Multiclass Classification
2.3.1 Multiclass


2.3.2 Softmax

- Softmax 회귀 알고리즘은 로지스틱 회귀의 일반화로, 다중 클래스 분류 문제에 적용된다.
- 로지스틱 회귀는 이진 분류 문제에서 y가 0 또는 1일 확률을 예측한다. 반면, softmax 회귀는 y가 0 또는 1일 확률을 예측한다.
- 반면, softmax 회귀는 y가 여러 값(예: 1, 2, 3, 4)을 가질 수 있을 때, 각 클래스에 대한 확률을 계산한다. 이는 각 클래스에 대해 z 값을 계산한 후, 이를 사용해 확률 ai를 구하는 방식이다. 모든 클래스의 확률 합은 1이 된다.
- softmax 회귀는 n개의 클래스를 처리할 수 있으며, n=2인 경우 로지스틱 회귀와 동일한 결과를 낸다.

- Softmax 회귀의 비용 함수는 각 클래스에 대한 확률 ai를 기반으로 한다.
- 로지스틱 회귀에서 비용 함수는 예측 확률 a1 a2를 사용하여 계산되었듯이, softmax 회귀에서도 유사하게 동작한다.
- y가 특정 클래스 j일 때 손실은 -log(aj)로 계산되며, 이는 aj가 클수록 손실이 작아지게 하여 모델이 정확한 클래스를 높은 확률로 예측하도록 유도한다.
- 전체 비용 함수는 모든 훈련 데이터에 대한 평균 손실로 정의된다.
2.3.3 Neural network with softmax output

- 다중 클래스 분류를 위한 신경망을 구축하려면 Softmax 회귀 모델을 출력층에 사용한다.
- 손글씨 숫자 인식에서 두 클래스만 다루던 신경망을 10개의 클래스(0부터 9까지)로 확장하려면, 출력층에 10개의 출력 유닛을 추가하고 Softmax 출력을 사용한다.
- 입력X에 대해 이전과 동일하게 첫 번째와 두 번째 숨겨진 층의 활성화 값을 계산한 후, 출력층의 활성화 값 a3를 계산한다.
- Softmax 출력층은 각 클래스에 대한 확률을 계산하며, 각 출력 ai는 모든 Z 값에 의존한다. 따라서 a1부터 a10까지의 값은 Z1부터 Z10까지의 값에 기반하여 동시에 계산된다.

[기본 코드 structure]
2.3.4 Improved implementation of softmax

- Softmax 층이 있는 신경망 구현에서 숫자를 계산할 때, 잘못된 방법으로 계산하면 수치적 반올림 오류가 발생할 수 있다.
- 예를 들어, 2/10,0002/10,0002/10,000을 직접 계산하는 방법은 정확하지만, 1+1/10,0001 + 1/10,0001+1/10,000에서 1−1/10,0001 - 1/10,0001−1/10,000을 뺀 결과로 계산하면 반올림 오류가 발생할 수 있다.
- 이는 컴퓨터의 유한한 메모리로 인해 발생하는 문제이다. 더 나은 구현을 위해서는 이러한 오류를 피할 수 있는 계산 방법을 선택해야 한다.

- Softmax 비용 함수의 계산에서 수치적 반올림 오류를 줄이기 위해, 기존의 중간 값을 명시적으로 계산하는 대신, TensorFlow가 직접 비용 함수를 계산하도록 하면 더 정확한 결과를 얻을 수 있다.
- 로지스틱 회귀에서 손실 함수 계산 시 중간 값 a를 계산하는 대신, 이를 포함한 표현식을 직접 사용하면 TensorFlow가 더 효율적으로 계산할 수 있다.
- 이는**output layer의 activation function을 ‘linear’**으로 바꾸고 from_logits=True 인자를 사용하여 구현할 수 있다. Softmax의 경우(Numberical Roundoff Error가 특히 두드러지기 때문에), 이러한 접근 방식이 수치적 오류를 더욱 효과적으로 줄여준다.

- Softmax 회귀에서 수치적 반올림 오류를 줄이기 위해, 활성화 값과 손실 함수를 별도로 계산하는 대신 TensorFlow가 직접 손실 함수를 계산하도록 지정하면 더 정확한 결과를 얻을 수 있다.
- 이를 위해 출력층에서 선형 활성화 함수를 사용하고, from_logits=True 인자를 사용하여 손실 함수를 설정한다.
- 이렇게 하면 TensorFlow가 중간 값을 효율적으로 처리하여 매우 작은 값이나 매우 큰 값으로 인한 오류를 피할 수 있다. 이 방식은 더 정확하지만 코드 가독성은 다소 떨어질 수 있다.
For softmax (multiclass classification)

For sigmoid (binary classification)

Just one more thing!!
- 출력층을 선형 활성화 함수로 변경하면, 신경망의 최종 출력은 확률이 아닌 z1에서 z10까지의 값이 되며, 확률을 얻기 위해서는 출력값을 적절한 함수로 변환해야 한다.
2.3.5 Classification with multiple outputs (optional)
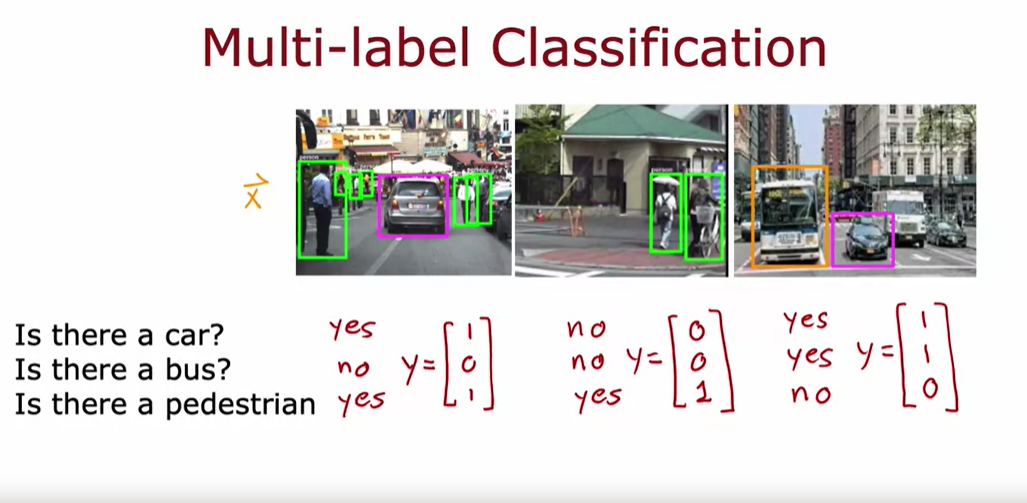
- 다중 클래스 분류와 달리, 다중 라벨 분류는 하나의 입력 이미지에 대해 여러 개의 라벨이 있을 수 있다.
- 예를 들어, 자율 주행 차의 경우 이미지에 차, 버스, 보행자가 있는지 각각 판단해야 한다.
- 다중 라벨 분류에서는 Y가 세 개의 숫자로 구성된 벡터가 되며, 각 숫자는 특정 객체의 존재 여부를 나타낸다.
- 이 문제를 해결하는 한 가지 방법은 각 객체에 대해 별도의 신경망을 구축하는 것이다.

- 다중 라벨 분류를 위해 하나의 신경망을 사용하여 동시에 여러 객체(차, 버스, 보행자)를 감지할 수 있다.
- 입력 X를 받아 첫 번째와 두 번째 숨겨진 층을 거쳐, 출력층에 세 개의 뉴런을 배치하고 각 뉴런에 sigmoid 활성화 함수를 사용하여 각각의 이진 분류 문제를 해결한다.
- 이를 통해 a3는 차, 버스, 보행자의 존재 여부를 나타내는 세 개의 숫자로 구성된 벡터가 된다. 다중 클래스 분류와 다중 라벨 분류의 차이를 이해하여 적절한 방법을 선택할 수 있다.
2.4 Additional Neural Networks Concepts
2.4.1 Advanced Optimization

- Adam 알고리즘은 비용 함수 최소화를 위해 학습률(Alpha)을 자동으로 조정하여 신경망 훈련을 가속화하는 최적화 알고리즘이다.
- Gradient descent는 일정한 학습률을 사용하지만, Adam은 작은 스텝이 반복되면 학습률을 키우고, 큰 스텝이 반복되면 학습률을 줄여 효율적으로 최소값에 도달하도록 한다.
- 이는 학습 속도를 높이고 진동을 줄여 더 안정적인 최적화를 가능하게 한다.

- Adam 알고리즘은 모델의 모든 파라미터에 대해 개별 학습률을 적용하여 더 효과적으로 최적화한다.
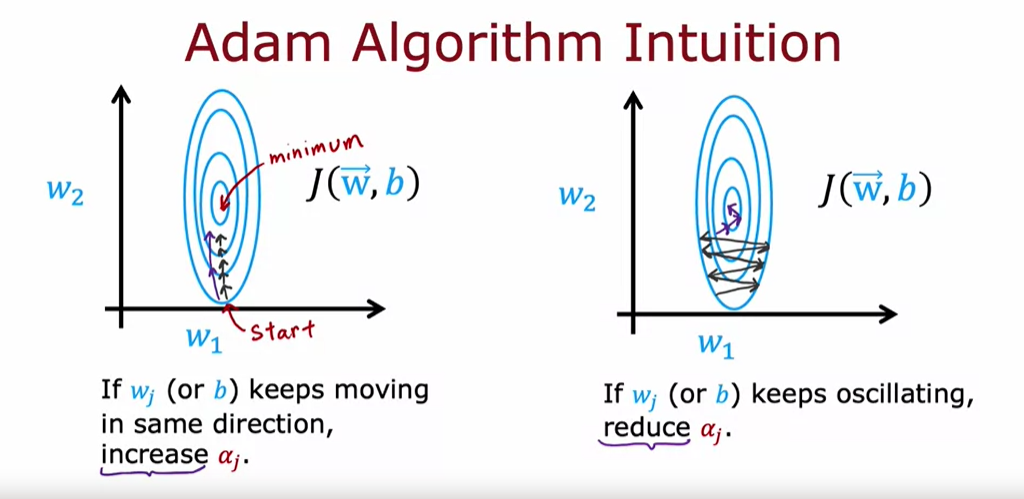
- Adam 알고리즘의 핵심 아이디어는 파라미터가 일정한 방향으로 계속 움직이면 학습률을 높여 더 빠르게 진행하고, 파라미터가 진동하면 학습률을 줄여 진동을 완화하는 것이다.
- Adam은 각 파라미터에 대해 개별적으로 학습률을 조정하여 최적화를 더욱 효율적으로 수행한다.

- Adam 최적화 알고리즘은 초기 학습률 α가 필요하며, 일반적으로 10^−3을 설정한다.
- 실제로 사용할 때는 여러 학습률을 시도해보며 가장 빠른 학습 성능을 찾는 것이 좋다.
- Adam은 학습률을 자동으로 조정하기 때문에, 기본 gradient descent 알고리즘보다 학습률 선택에 덜 민감하다. 하지만 여전히 학습률을 조정해 최적의 성능을 찾는 것이 필요하다.
Additional Layer Types

- Dense layer의 경우, 두 번째 숨겨진 층의 뉴런 활성화 값은 이전 층의 모든 활성화 값의 함수이다.
- 하지만 특정 상황에서는 다른 유형의 층을 사용할 수도 있다.
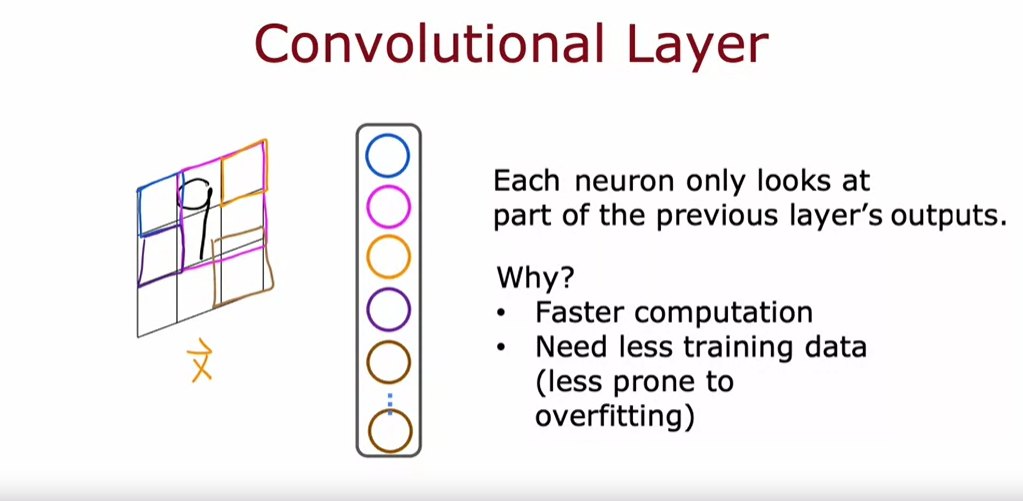
- Convolutional layer는 입력 이미지의 일부 영역만을 보는 뉴런들로 구성된다.
- 예를 들어, 손글씨 숫자 9의 이미지를 처리할 때, 각 뉴런이 이미지의 작은 부분만을 관찰한다.
- 이렇게 하면 계산 속도가 빨라지고, 필요한 학습 데이터가 줄어들며 과적합 가능성이 감소한다.

- Convolutional neural network(CNN)은 여러 convolutional layer로 구성된 신경망이다.
- 예를 들어, EKG 신호 분류에서 각 convolutional layer의 뉴런은 입력 신호의 일부 영역만 본다.
- 첫 번째 숨겨진 층의 뉴런은 입력 신호의 작은 창을 보고, 두 번째 숨겨진 층의 뉴런은 이전 층의 일부 활성화 값만 본다.
- 마지막으로 출력층은 모든 값을 보고 이진 분류를 수행한다.
- Convolutional layer는 창 크기와 뉴런 수 등 다양한 설계 선택이 가능하여, 특정 응용 분야에서 dense layer보다 더 효과적일 수 있다.
2.5 Back Propagation (Optional)
2.5.1 What is derivative (optional)


[sympy package for get derivatives in code]

2.5.2 Computation graph (Optional)
[Forward Prop(Getting loss and cost value from left to right)] 🔥🔥🔥

[Backward Prop(Getting derivatives from right to left)] 🔥🔥🔥

[Double Checking the Calculation]

[why going right to left?] 🔥🔥

- Backpropagation은 derivatives를 효율적으로 계산하는 방법으로, 오른쪽에서 왼쪽으로 계산을 수행한다.
- 이는 각 중간 값의 변화가 최종 output j에 미치는 영향을 순차적으로 계산하기 때문이다.
- 이 방법은 각 중간 값의 derivatives를 한 번만 계산하여 모든 파라미터에 대한 derivatives를 효율적으로 계산할 수 있게 한다.
- 따라서, n개의 노드와 p개의 파라미터를 가진 신경망에서n+p 단계로 derivatives를 계산할 수 있어,n×p 단계가 필요한 경우보다 훨씬 빠르다.
2.5.3 Larger neural network example (Optional)


'AI Study' 카테고리의 다른 글
| Advanced Learning Algorithms #4 (Decision Tree Model ) (0) | 2024.07.06 |
|---|---|
| Advanced Learning Algorithms #3 (Advice for Applying Machine Learning) (0) | 2024.07.04 |
| Advanced Learning Algorithms #1 (Neural Networks) (0) | 2024.07.01 |
| Supervised Machine Learning Regression and Classification #2 (0) | 2024.06.29 |
| Supervised Machine Learning Regression and Classification #1 (0) | 2024.06.26 |



