1. Classification with logistic regression
1.1 Motivation


- linear regression을 classification 문제에 사용할 수 없는 이유!
- linear regression을 사용한 다음, threshold를 설정해서 0.5 이상 일경우 True, 0.5미만일 경우 False 하는 방식으로 구상
- 하지만 위와 같이, 오른쪽에 data point가 하나가 더 추가된다면, decision boundary가 오른쪽으로 밀리게 되고, 여러 개의 data point가 misclassified된다는 것을 알 수 있다!
1.2 Logistic Regression






1.3 Cost Function for Logistic Regression

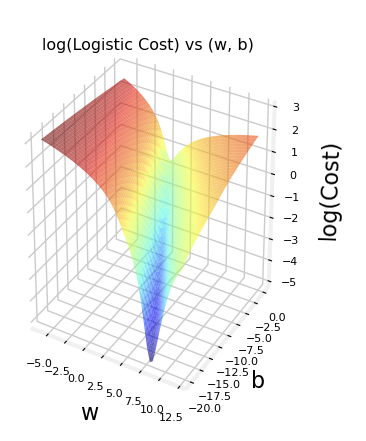
- In Linear regression model, we used squared error cost function and it gave a nice convex shape.
- But if we use square error cost function on logistic regression model, it does not give a convex-shape and gives us a lot of local minima
- Thus, squared error cost function is not appropriate for logistic regression
- Summation 내의 내부의 항을 단일 학습 예제에 대한 손실(loss on a single training example)로 정의하며, 이를 L로 표시
- 손실 함수의 형태를 다르게 선택함으로써 전체 비용 함수가 볼록 함수로 유지될 수 있음!
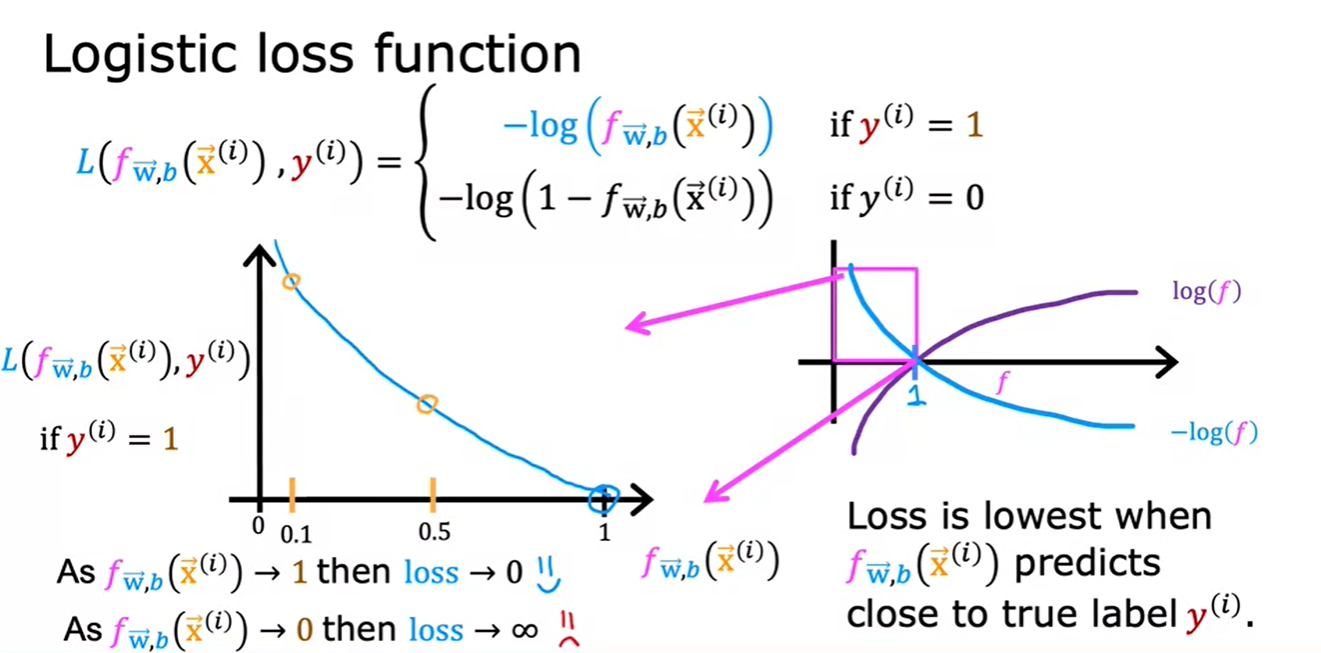
- logistic regression(f)는 0과 1사이의 값만 가지므로 저 핑크 박스 부분만 보면 된다.
- yi=1일 경우, f(예측값)이 1일때 Loss가 0인 모습을 볼 수 있다.
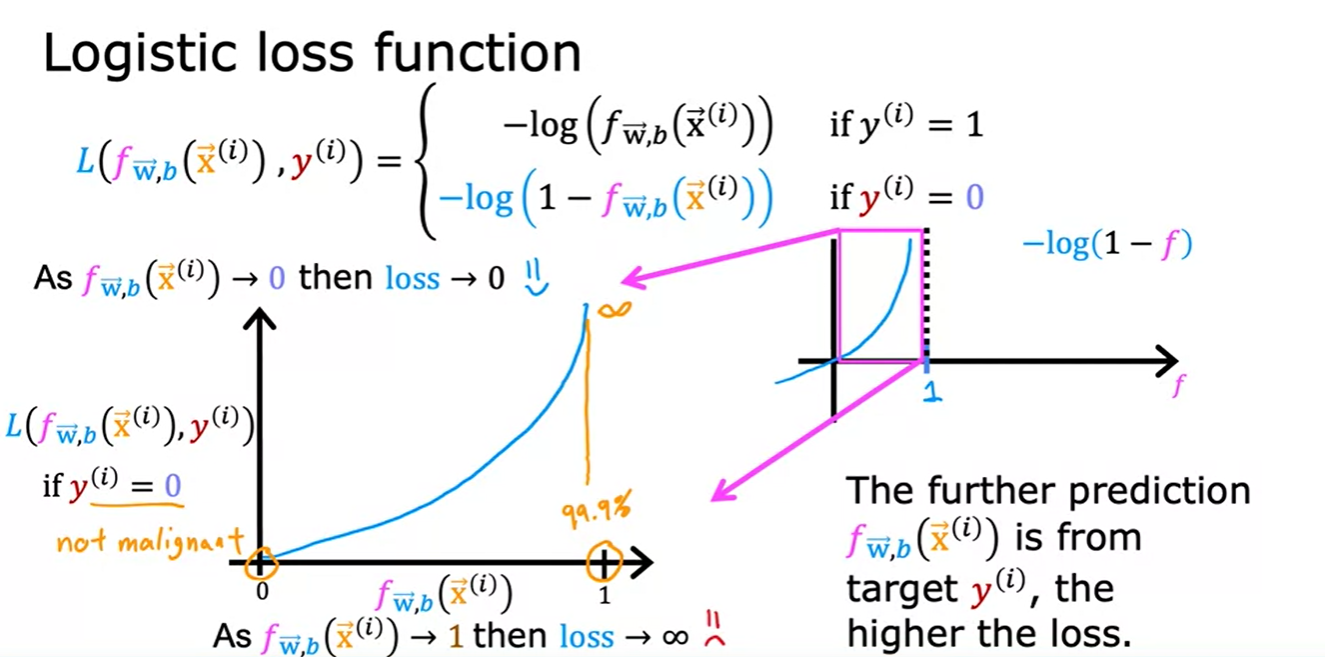
- yi=0일 경우, f(예측값)이 0일때 Loss가 0인 모습을 볼 수 있다.
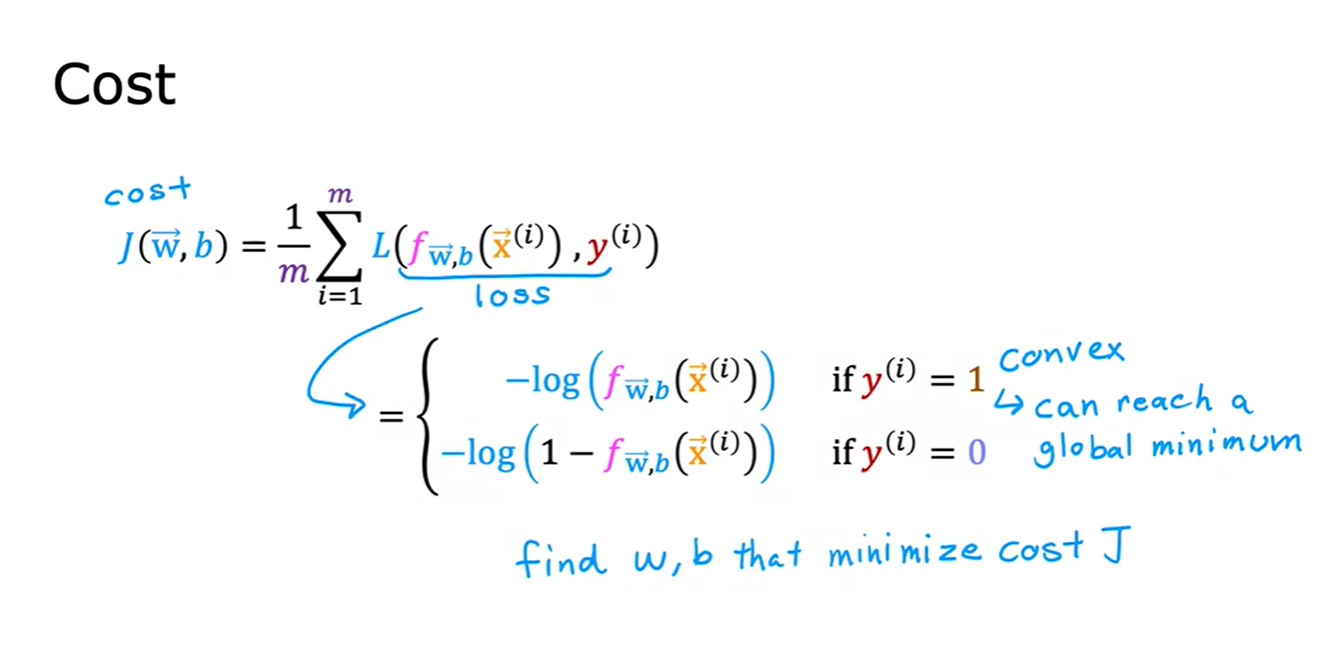
- 이러한 loss function을 통해 convex인 cost function을 만들 수 있고 global minimum을 gradient descent를 통해 도달할 수 있다!!
1.4 Simplified Loss Function

- 이렇게 한 줄로 간단하게 표현할 수 있다!

- 많은 가능성있는 cost function 중에 logistics regression의 cost function으로 선택된 이유가 무엇일까?
- The cost function is derived from statistics, specifically using the principle of maximum likelihood estimation (MLE)
- 최대 가능도 추정(MLE, Maximum Likelihood Estimation)은 주어진 데이터에 가장 잘 맞는 모델 파라미터를 찾기 위해 가능도를 최대화하는 통계적 방법이다.
요약

2. Gradient Descent for Logistics Regression
2.1 Gradient descent implementation


2.2 The problem of overfitting
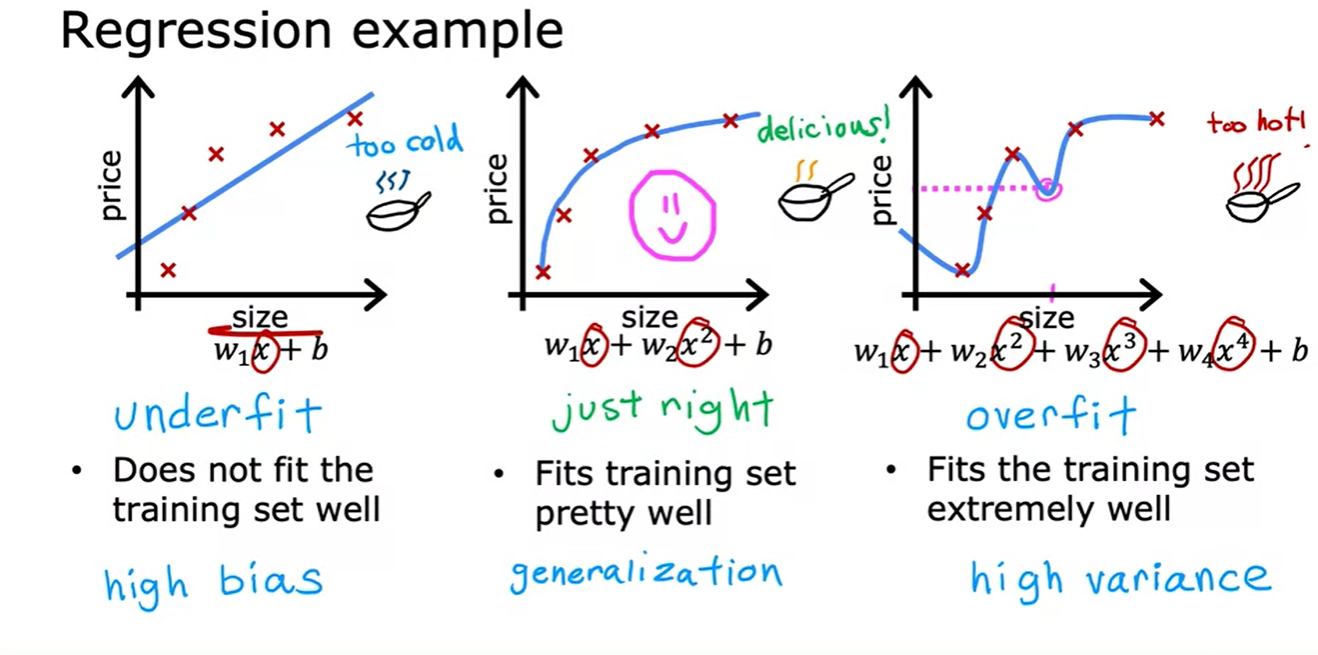
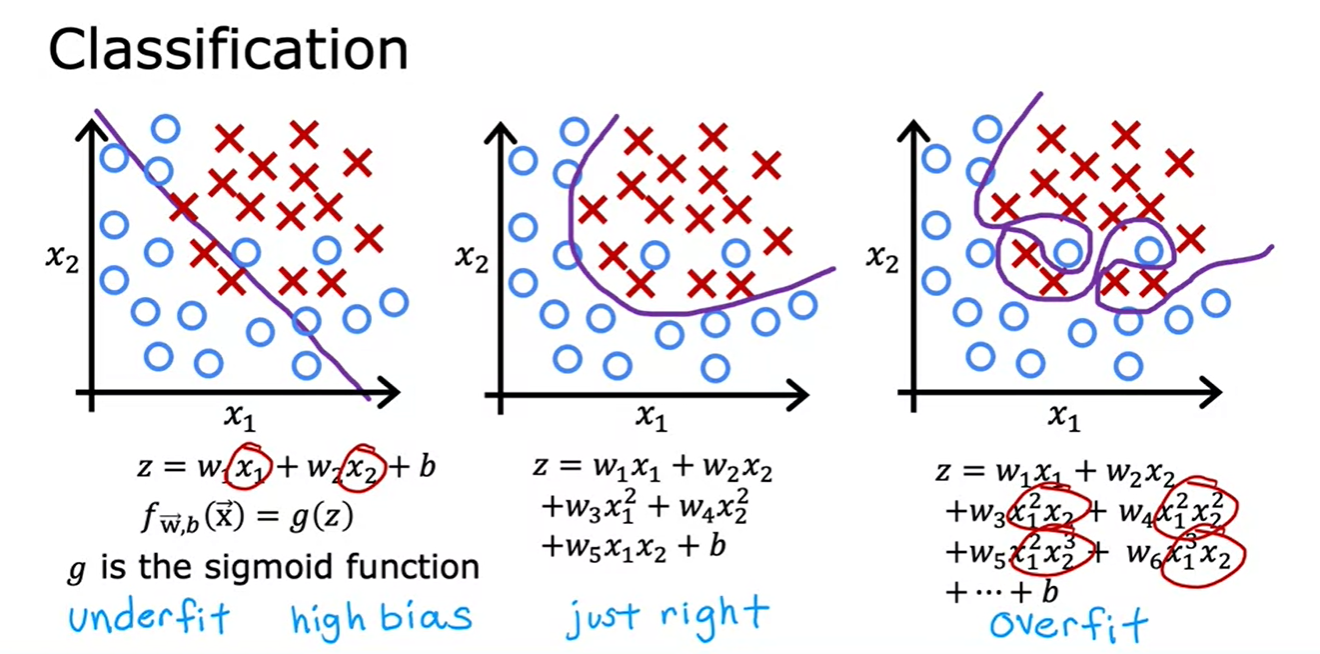
2.3 Addressing overfitting
1. collect more training examples
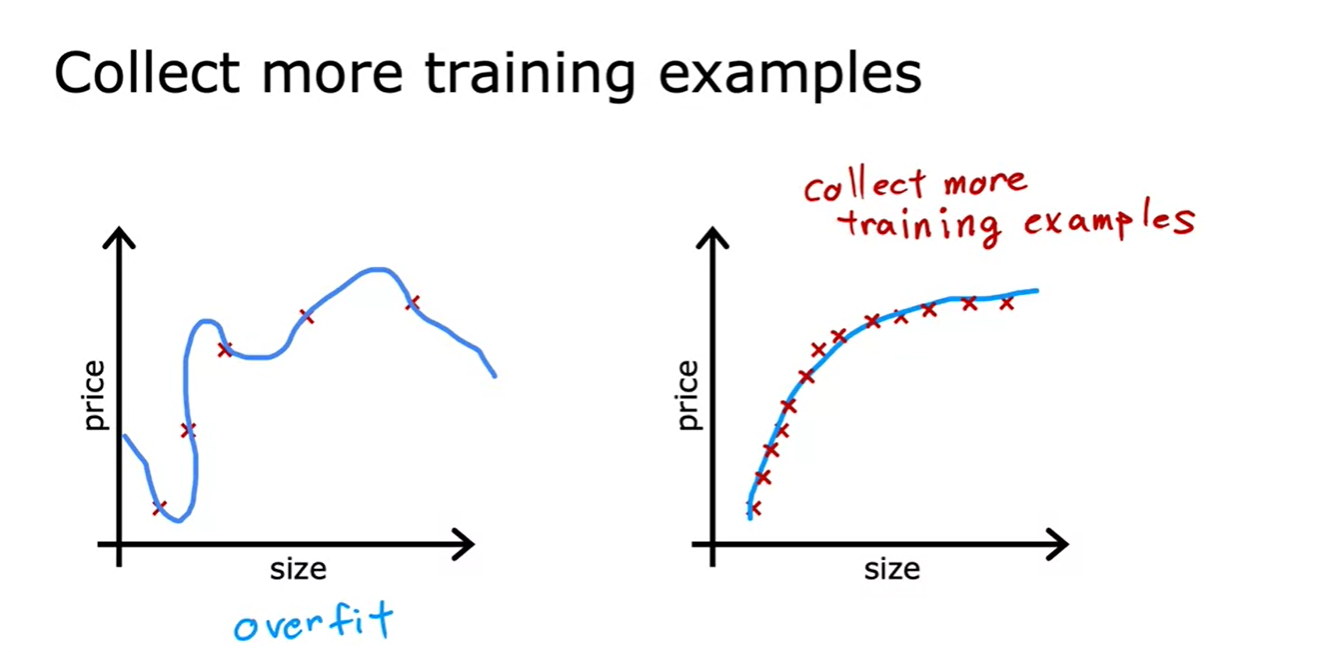
2. select features to include/exclude
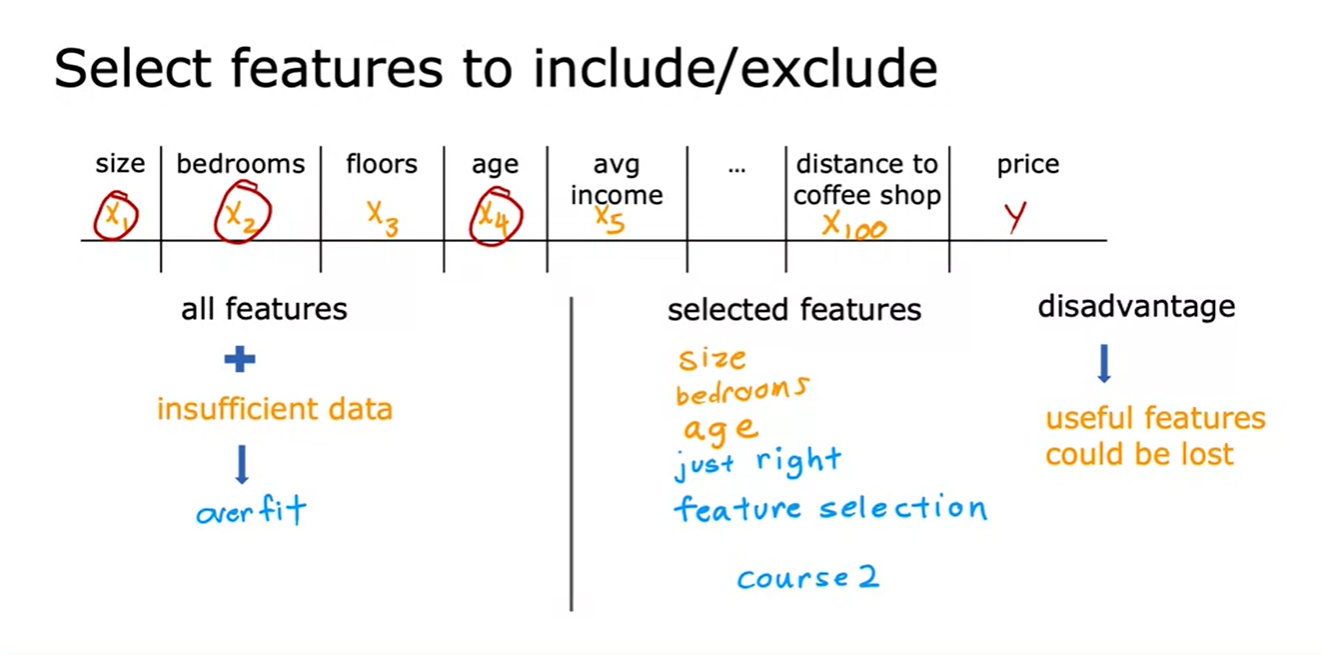
- In course2, we’ll go over how to automatically select features that are relevant
3. Regularization
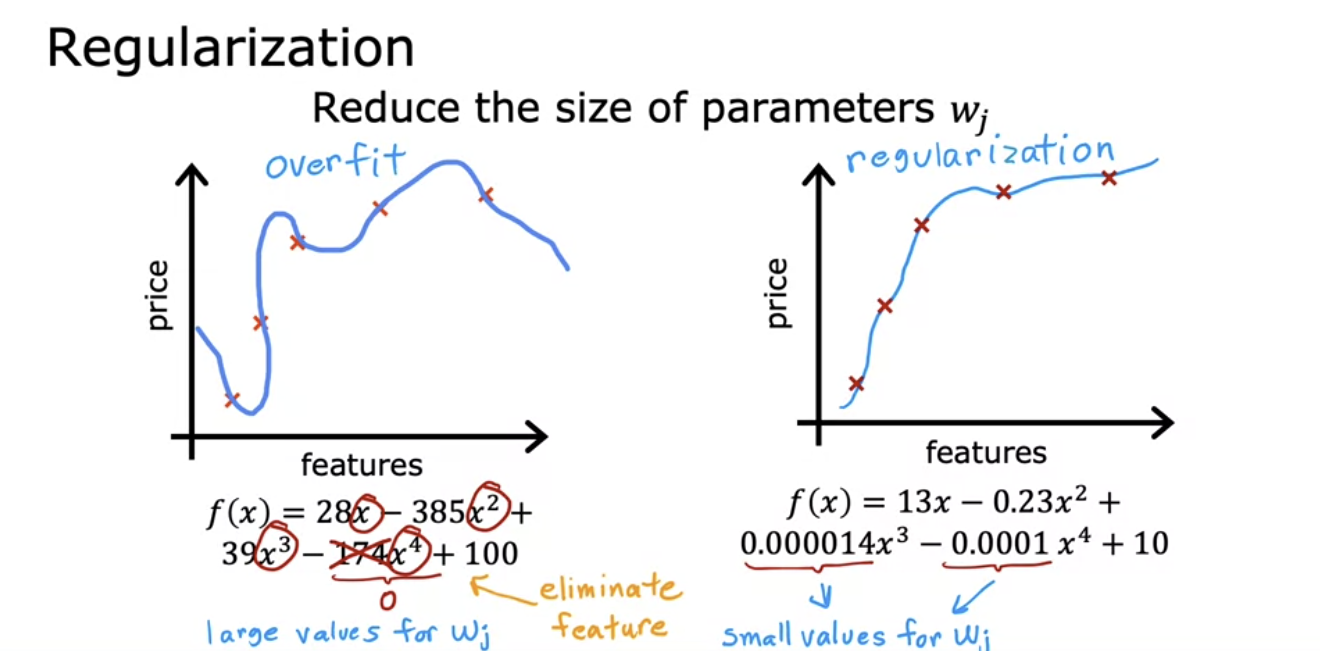
- So what regularization does, is it lets you keep all of your features, but they just prevents the features from having an overly large effect, which is what sometimes can cause overfitting.

2.4 Cost Function with Regularization
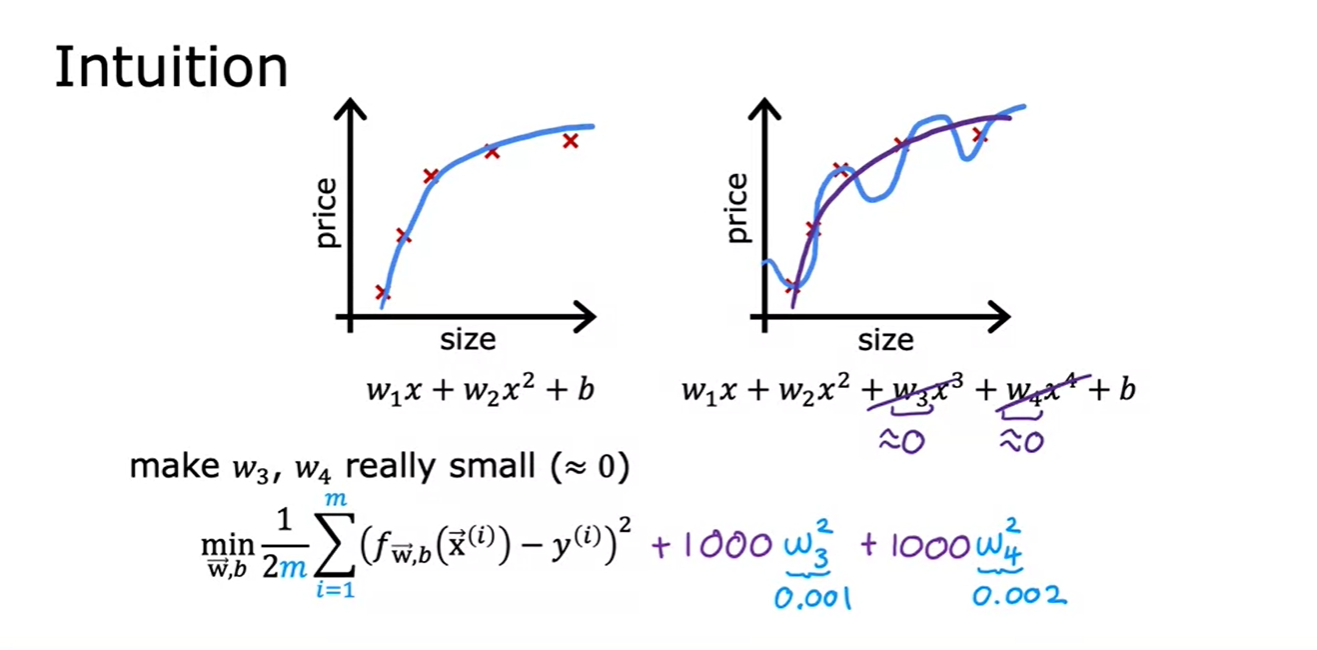
- Cost Function에 저런 항들을 추가시켜서 w3과 w4의 크기에 큰 제약을 줄 수가 있다.
- 일반적으로는 **모든 wj 파라미터(어느 파라미터가 중요하고 아닌지 모르기 때문에)**를 페널티하여 과적합을 방지하고 더 부드럽고 단순한 함수를 만듦

- b를 regularize해도 되고 안해도 됨. (결과에 큰 영향을 주지 않음)
- 정규화 항을 포함한 비용 함수에서 λ를 2m으로 나누어 모든 항을 동일하게 스케일링하면, λ의 값을 선택하기가 더 쉬워지고, 훈련 세트 크기(m)가 증가해도 이전에 선택한 λ 값이 계속 유효할 가능성이 높아집니다.

- λ는 0이면 과적합되고, 너무 크면 과소적합되므로, 평균 제곱 오차를 최소화하면서 파라미터를 적절히 조절하는 중간 값이 필요합니다.
2.5 Regularized Linear Regression


- 알파(α)는 작은 양수로, 예를 들어 0.01이며, 람다(λ)는 일반적으로 작은 수로, 예를 들어 1로 설정한다면,
- 훈련 세트 크기(m)가 50일 때, αλ/m은 작은 양수인 0.0002가 된다.
- 매번 경사 하강법 반복 시 w_j를 0.9998로 곱해 w_j 값을 조금씩 줄이는 효과가 있다.
- 따라서 정규화는 매 반복마다 파라미터 w_j를 약간씩 감소시킨다.
2.6 Regularized Logistics Regression
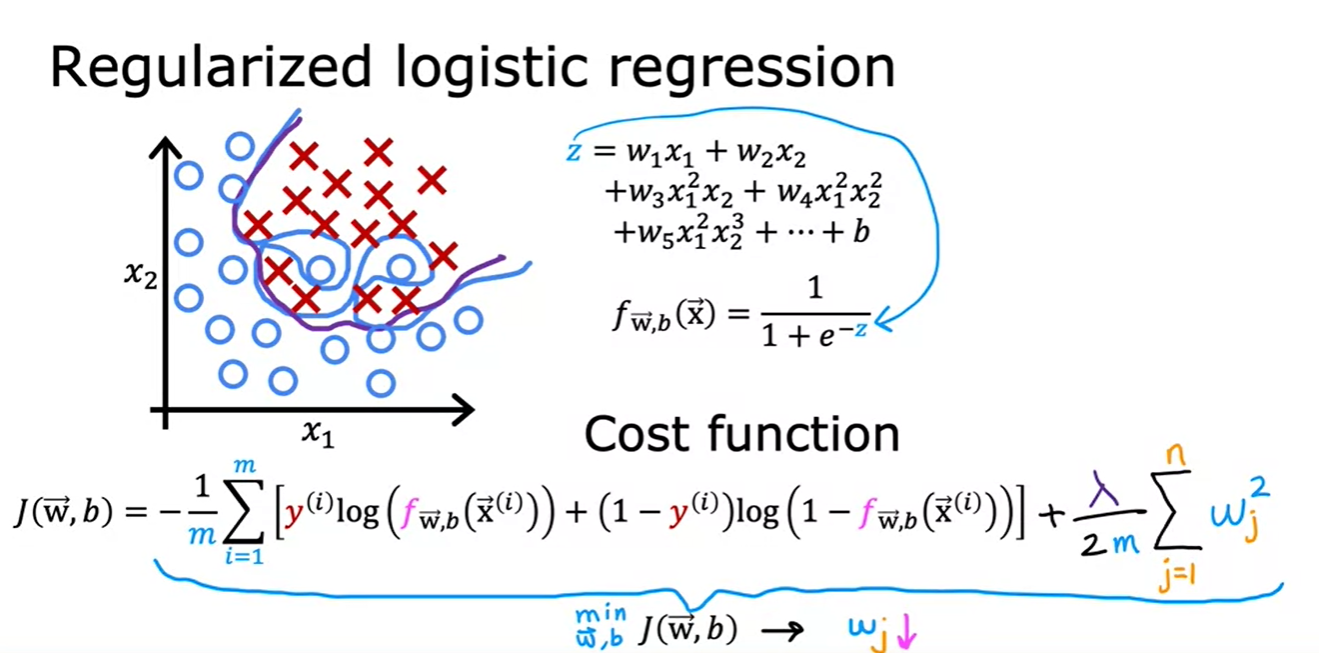
- 과적합된 logistic regression 모델에서도 정규항을 추가해 모든 피쳐들을 유지하면서도 좋은 generalization 모델을 만들 수 있다.
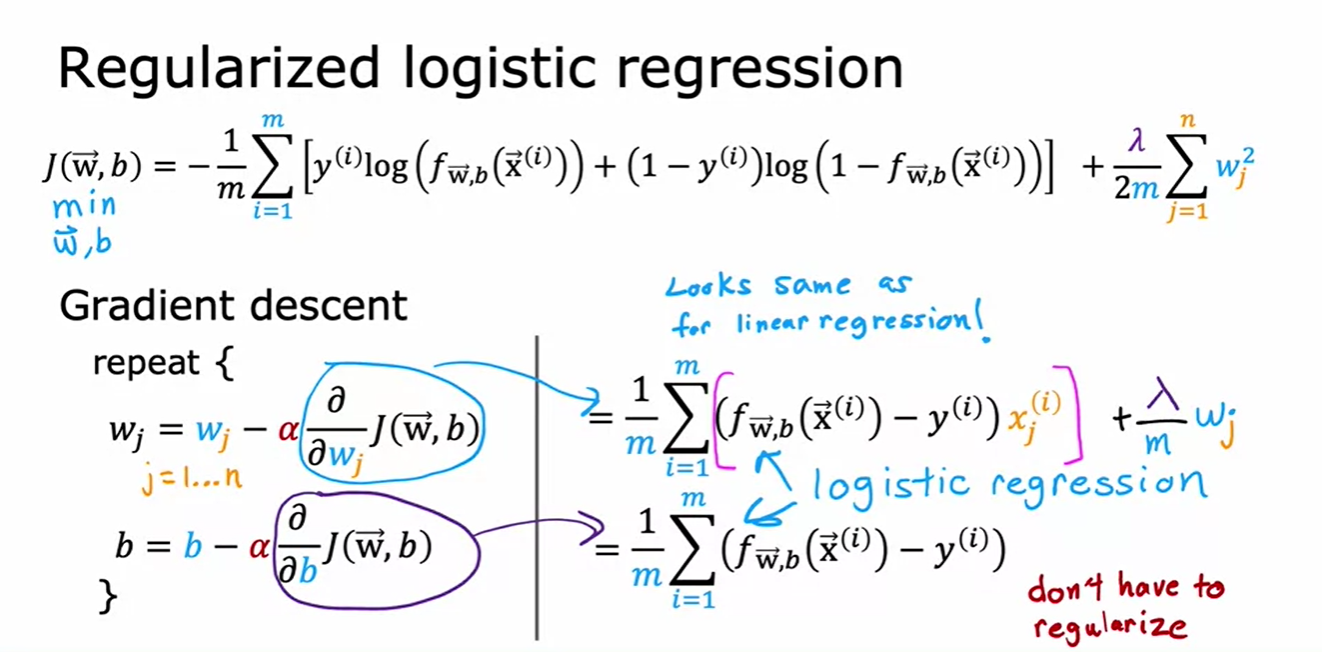
- They look very similar to gradient descent for regularized linear regression, only f(x) is not the same
'AI Study' 카테고리의 다른 글
| Advanced Learning Algorithms #4 (Decision Tree Model ) (0) | 2024.07.06 |
|---|---|
| Advanced Learning Algorithms #3 (Advice for Applying Machine Learning) (0) | 2024.07.04 |
| Advanced Learning Algorithms #2 (Neural Network Training) (0) | 2024.07.02 |
| Advanced Learning Algorithms #1 (Neural Networks) (0) | 2024.07.01 |
| Supervised Machine Learning Regression and Classification #1 (0) | 2024.06.26 |



