1.1 Neural Networks Intuition
1.1.1 Neurons and Brains


Simplified Diagram of biological neuron


- 최근 몇 년 동안, 디지털 데이터의 폭발적인 증가와 함께 전통적인 머신러닝 알고리즘(로지스틱 회귀, 선형 회귀)이 대규모 데이터에서 성능을 향상시키지 못하는 한계를 보였다.
- 반면, 신경망(특히 대형 신경망)은 많은 데이터를 효과적으로 활용하여 성능을 지속적으로 향상시킬 수 있었으며, GPU와 같은 빠른 컴퓨터 프로세서의 발전도 딥러닝 알고리즘의 발전에 기여했다.
1.1.2 Demand Prediction

- 로지스틱 회귀를 통해 sigmoid 함수(f(x))를 적용해 예측 가능, 출력값 a(활성화)로 변환하여 단일 뉴런의 모델로 사용. 신경망은 이러한 뉴런들을 결합하여 구성.

- 층(Layer) 개념: 입력층, 숨겨진 층, 출력층. 각 층은 특징 벡터를 입력받아 활성화 값을 출력. 중간 층은 입력 특징을 처리해 더 나은 예측 기능 학습.
- Intuition: 신경망은 입력 특징을 처리하여 중간 층을 통해 자동으로 유용한 특징을 학습하고 최종 예측을 수행하는 강력한 학습 알고리즘 🚀🚀🚀
- 결국 뒤의 두 층만 본다면, 이는 affordability, awareness, perceived quality라는 특징(feature)들을 x값으로 한 logistics regression인 셈이다. 그렇다면 결국 신경망은 입력 특징을 처리하여 top seller를 예측하기 위한 더 나은 특징들을 만들어내는 즉, 자동 feature engineering 기능이 탑재되어 있는 machine learning인 셈이다 ‼️ 🔥🔥🔥
- **숨겨진 층(hidden layer)**이란 이름이 붙은 이유는, 학습 데이터 세트에는 입력값(x)과 출력값(y)만 있고 중간 계산 값인 활성화 값(affordability, awareness, perceived quality 등)은 포함되어 있지 않기 때문이다. 이 중간 값들은 학습 데이터에서 직접 관찰할 수 없고 숨겨져(hidden) 있기 때문에 숨겨진 층이라고 부른다.
이번에는 hidden layer가 여러 개인 case를 살펴보자!

- 예시 설명: 입력 특징 벡터 X를 첫 번째 숨겨진 층에 입력. 첫 번째 숨겨진 층의 출력은 두 번째 숨겨진 층에 입력되고, 그 후 출력층에서 최종 예측값을 출력.
- **멀티레이어 퍼셉트론: 여러 숨겨진 층을 가진 신경망을 멀티레이어 퍼셉트론(MLP)**이라고 부름.
- 구조 결정: 신경망을 설계할 때, 숨겨진 층의 개수와 각 층의 뉴런 수를 결정해야 함. 이는 신경망의 아키텍처에 해당.
- 성능 영향: 숨겨진 층의 개수와 뉴런 수는 학습 알고리즘의 성능에 영향을 미침!!
- 추후 학습: 적절한 신경망 아키텍처를 선택하는 팁은 코스 후반부에 배울 수 있음.
Example: Recognizing Images

- 얼굴 인식 애플리케이션에서는 1,000x1,000 픽셀 이미지의 밝기 값(즉, 100만개의 픽셀값)을 벡터로 변환하여 신경망에 입력하고, 이를 통해 인물의 신원을 출력하도록 훈련한다.

- 신경망은 여러 숨겨진 층을 통해 이미지 특징을 추출한다.
- 첫 번째 숨겨진 층은 짧은 선이나 모서리를 감지하고, 두 번째 층은 눈, 코 등 얼굴의 일부분을 감지한다. ****세 번째 층은 더 큰 얼굴 형태를 인식하며, 최종 출력 층은 이를 바탕으로 인물의 신원을 예측한다.
- 신경망은 이러한 특징 감지기를 데이터로부터 자동으로 학습한다.
1.2 Neural Network Model
1.2.1 Neural Network Layer

- 예제 설명: 수요 예측 예제에서 4개의 입력 특징이 3개의 뉴런으로 구성된 숨겨진 층에 입력되고, 출력층으로 전달되어 최종 예측값을 출력함.
- 숨겨진 층 계산: 각 뉴런은 로지스틱 회귀 유닛을 구현하며, 입력값에 가중치(w)와 편향(b)을 적용하여 활성화 값(a)을 계산함.
- 계층 표기법: 입력층을 0층, 첫 번째 숨겨진 층을 1층, 두 번째 숨겨진 층을 2층 등으로 표기. 각 층의 출력은 다음 층의 입력으로 사용됨.
- 활성화 값 계산: 예를 들어, 첫 번째 뉴런은 a_1 = g(w_1 · x + b_1), 두 번째 뉴런은 a_2 = g(w_2 · x + b_2), 세 번째 뉴런은 a_3 = g(w_3 · x + b_3)으로 계산됨.
- 층 구분: 각 층의 활성화 값과 파라미터에 대해 상위첨자 표기법(예: a^[1], w^[1], b^[1])을 사용하여 다른 층과 구분함.

- 2층이자 출력층의 계산에서, 첫 번째 층의 출력인 벡터 a^[1]을 입력으로 받아, 단일 뉴런이 sigmoid 함수 g(w^[2] · a^[1] + b^[2])를 적용하여 최종 출력값 a^[2]을 계산.

- 신경망이 a^[2]를 계산한 후, 0.5를 기준으로 이 값을 이진 예측(0 또는 1)으로 변환하여 최종 예측값 y^를 결정할 수 있음!
1.2.2 More Complex Neural Networks

1.2.3 Inference: Making Predictions (forward propagation)


- 글자 이미지 인식 예제를 통해, 8x8 이미지(64픽셀)를 입력으로 받아, 신경망을 이용해 0 또는 1로 분류하는 방법을 설명
- 첫 번째 층은 25개의 뉴런, 두 번째 층은 15개의 뉴런, 출력층은 1개의 뉴런으로 구성
- 입력값 X로부터 a1, a2를 거쳐 최종 출력값 a3를 순차적으로 계산하며, 최종적으로 a3을 0.5로 임계값 처리해 이진 분류를 수행 (이를 왼쪽에서 오른쪽으로 순차적으로 계산 및 진행한다고 하여 **순전파(forward propagation)**라고함)
1.3 TensorFlow Implementation
1.3.1 Inference In Code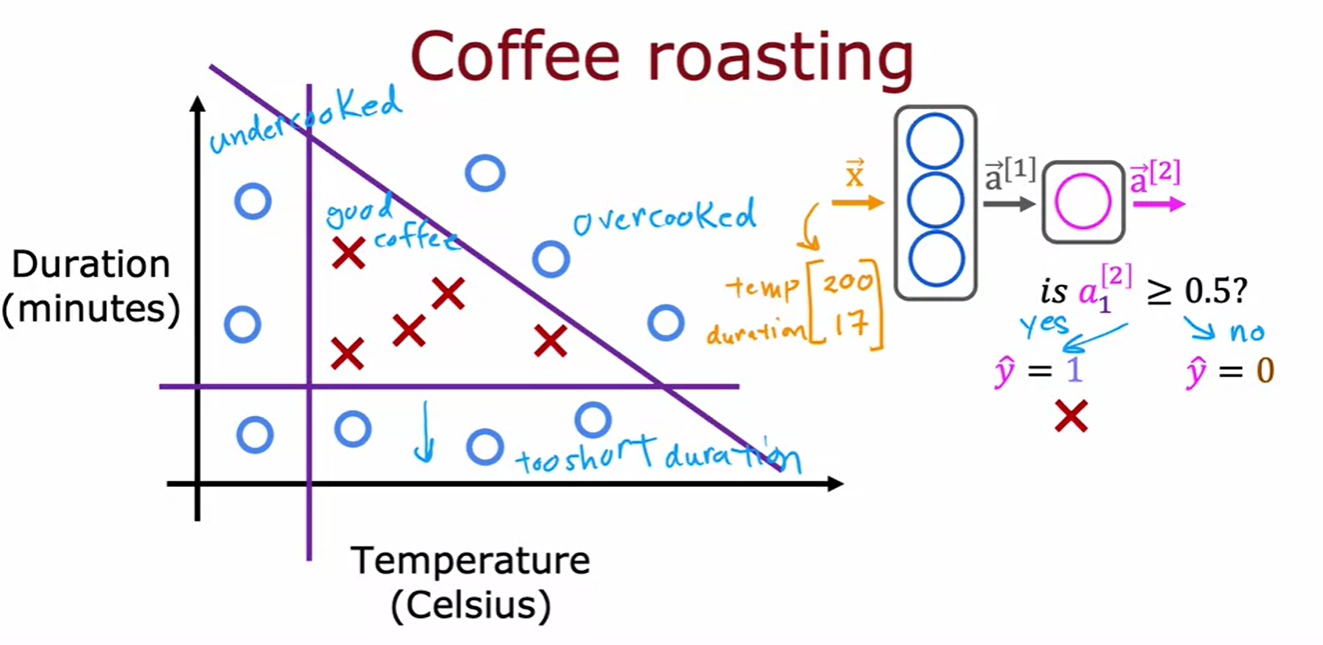
- how can we do inference in a neural network to get it to tell us whether or not this temperature and duration setting will result in good coffee or not?

- Tensorflow로 모델 빌딩하는 가장 기본 코드 방법!
- 커피 로스팅 최적화를 위한 신경망 예제에서, 입력 특징 벡터 x(온도 200도, 시간 17분)를 통해 좋은 커피가 될지 예측한다.
- 첫 번째 숨겨진 층(Layer 1)은 세 개의 뉴런과 sigmoid 활성화 함수를 사용해 a1(0.2, 0.7, 0.3)을 계산한다.
- 두 번째 숨겨진 층(Layer 2)은 한 개의 뉴런과 sigmoid 활성화 함수를 사용해 a2(0.8)을 계산한다.
- 마지막으로 a2를 0.5 임계값으로 이진 분류한다.
1.3.2 Data in TensorFlow


- [[200, 17]]은 1x2 행렬(행 벡터), [[200], [17]]은 2x1 행렬(열 벡터)을 생성합니다.
- 1D 벡터는 행과 열 개념이 없는 단순한 숫자 리스트입니다.
- TensorFlow는 대규모 데이터셋 처리를 위해 1D 배열 대신 행렬을 사용하여 효율성을 높입니다.

- a1은 layer 1을 x에 적용한 결과로, 1x3 행렬이다.
- TensorFlow에서 a1은 tf.tensor로 표시되며, 이는 32비트 부동 소수점 숫자로 구성된 1x3 행렬이다.
- TensorFlow의 텐서는 행렬을 효율적으로 저장하고 계산하는 데이터 타입이다.
- NumPy와 TensorFlow는 서로 다른 방식으로 행렬을 표현하며, TensorFlow 텐서를 NumPy 배열로 변환하려면 a1.numpy()를 사용하면 된다.

- a2는 1x1 행렬이다.

- 이전에는 각 층을 수동으로 만들고 데이터를 통과시키는 방식으로 순전파를 했지만, 이제 Sequential 함수를 사용해 층을 연결하여 신경망을 쉽게 구축할 수 있다.
- 훈련 데이터(X, Y)를 NumPy 배열로 저장한 후, model.compile과 model.fit 함수를 사용해 신경망을 훈련할 수 있다.
- 새로운 데이터에 대해 예측하려면 model.predict를 호출하면 된다.

- 추가적으로, TensorFlow 코드에서는 층을 변수에 할당하지 않고, Sequential 모델로 바로 정의하는 것이 일반적이다.
- 예를 들어, 모델을 Sequential로 정의하고 그 안에 각 dense 층을 설정하는 것으로 코드를 간소화할 수 있다.
예시

1.4 Neural Network Implementation in Python
1.4.1 Forward prop in a single layer

1.4.2 General Implementation of forward propagation

이번 영상에서는 Python으로 일반적인 순전파 구현을 설명한다. 핵심은 dense 함수를 작성해 신경망의 단일 층을 구현하는 것이다. dense 함수는 이전 층의 활성화 값과 현재 층의 파라미터(w와 b)를 입력으로 받아 현재 층의 활성화 값을 출력한다.
코드의 주요 단계는 다음과 같다:
- units를 설정해 현재 층의 유닛 수를 파악한다.
- a를 유닛 수에 맞게 0으로 초기화한다.
- for 루프를 통해 각 유닛의 활성화 값을 계산한다:
- 각 열을 w로 추출해 z 값을 계산하고, sigmoid 함수 g를 적용해 활성화 값을 얻는다.
- 마지막으로 활성화 값 벡터 a를 반환한다.
이 dense 함수를 사용해 신경망의 여러 층을 순차적으로 연결하여 순전파를 구현할 수 있다. 입력 특징 x에서 시작해 각 층의 활성화 값을 계산하고, 최종 출력 f(x)를 반환한다.
1.5 Vectorization (Optional)
1.5.1 How neural networks are implemented efficiently

- Much simpler code just by using 2D array and matrix multiplication
1.5.2 Matrix Multiplication
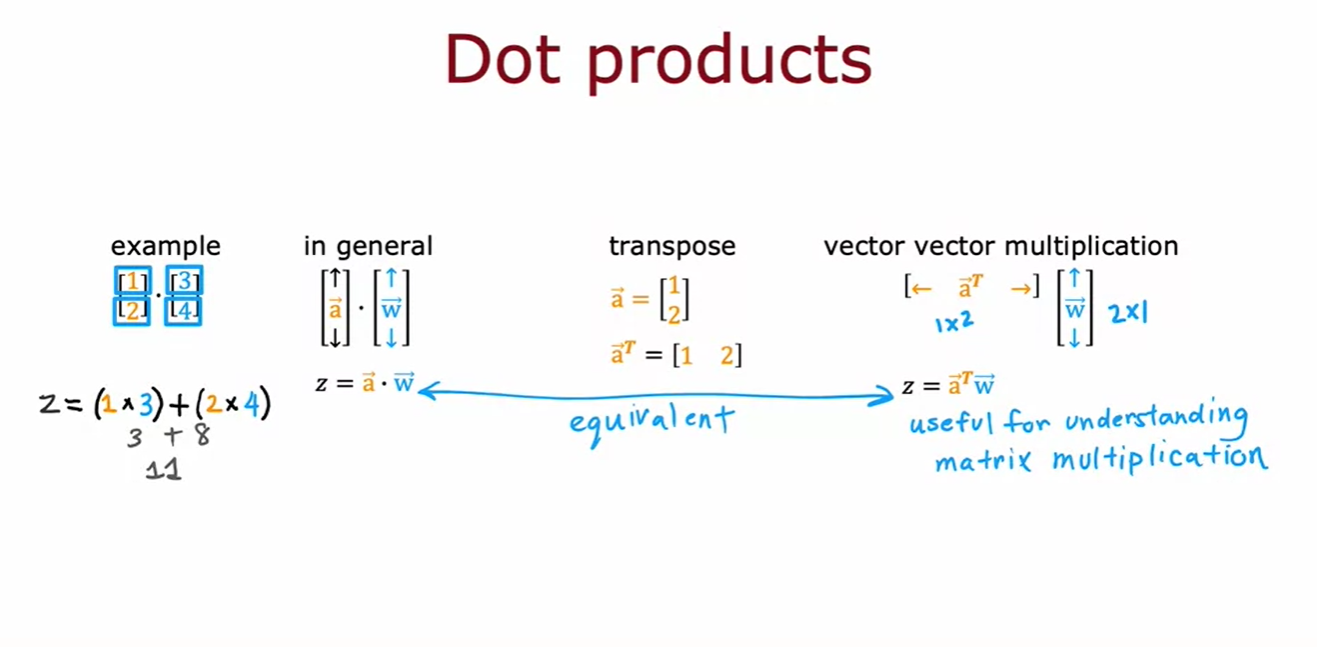
- 벡터의 내적(dot product)은 두 벡터의 각 요소를 곱한 후 합하는 것이다.
- 벡터의 내적(dot product)은 두 벡터의 각 요소를 곱한 후 합하는 것이다. 예를 들어, 벡터 (1, 2)와 (3, 4)의 내적은 13 + 24 = 11이다.
- 이는, 벡터 a의 전치(transpose)를 취해 행 벡터로 만들고, 이를 벡터 w와 곱하는 결과와 같다. (vector vector multiplication)
- 즉, a와 w의 내적은 z = a^T * w와 같다. 이는 행렬 곱셈을 이해하는 데 유용하다.


1.5.3 Matrix multiplication rules


1.5.3 Matrix multiplication code


'AI Study' 카테고리의 다른 글
| Advanced Learning Algorithms #4 (Decision Tree Model ) (0) | 2024.07.06 |
|---|---|
| Advanced Learning Algorithms #3 (Advice for Applying Machine Learning) (0) | 2024.07.04 |
| Advanced Learning Algorithms #2 (Neural Network Training) (0) | 2024.07.02 |
| Supervised Machine Learning Regression and Classification #2 (0) | 2024.06.29 |
| Supervised Machine Learning Regression and Classification #1 (0) | 2024.06.26 |



